Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 17.Problemas - Ex. 31

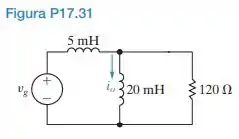
a) Use o método da transformada de Fourier para calcular I 0 no circuito da Figura P17.31, se v g   =   125   c o s   40000 t   V .

b) Verifique a resposta obtida em (a) determinando a expressão de regime permanente para I 0 , usando a análise fasorial.

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Fourier!

  1. Desenvolvendo o sistema acima, temos que:

    2. Podemos ver então que:

    V 0 - V g s L 1 + V 0 s L 2 + V 0 R = 0

    Logo:

    V 0 = R V g L 1 s + R 1 L 1 + 1 L 2

    Com isso:

    I 0 = V 0 s L 2

    Com isso:

    H s = I 0 V g = R / L 1 L 2 s ( s + R 1 L 1 + 1 L 2 = 12 x 10 5 s ( s + 3 x 10 4 )

    Temos então:

    H j ω = 12 x 10 5 j ω ( j ω + 3 x 10 4 )

    V g ω = 125 π δ ω + 4 x 10 4 + δ ( ω - 4 x 10 4 )

    Logo:

    I 0 ω = H j ω I g ω

    I 0 ω = 1 500 π x 10 5 δ ω + 4 x 10 4 + δ ( ω - 4 x 10 4 ) j ω ( j ω + 3 x 10 4 )

    Portanto:

    i 0 t = 0,075 c o s ⁡ ( 40000 t t - 143 , 13 ° ) A

    Passo 2

  2. Na fase dominante, temos que:

Podemos ver então que:

V 0 - 125 j 200 + V 0 j 800 + V 0 120 = 0

Com isso, temos:

V 0 = 1500 15 + j 20 = 60 / - 53,13 ° V

Portanto:

I 0 = V 0 j 800 = 75 x 10 - 3 / - 143,13 ° A

Por fim:

i 0 t = 75 cos ⁡ 40000 t - 143,13 ° m A

Resposta

  1. Item a:

    2. i 0 t = 0,075 c o s ⁡ ( 40000 t t - 143,13 ° ) A

  2. Item b:

i 0 t = 75 cos ⁡ 40000 t - 143,13 ° m A