Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 18.3 - Ex. 4

Use o resultado do Ex. 18.3.3 e (18.9), que, por causa da descontinuidade, escrevemos como,

Para deduzir onde

Passo 1

Fala aí pessoal tudo blz?

Nessa questão ele pede para usar os resultados,

para deduzir

onde,

Só vem meu camarada.

Passo 2

Sabendo que,

Lembrando que vale lembrar as transformações de Laplace que valem,

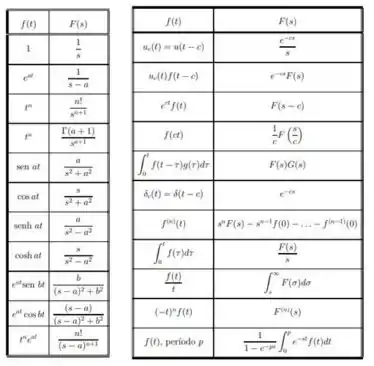
Temos,

Espero ter ajudado, bons estudos e até a próxima.

Resposta