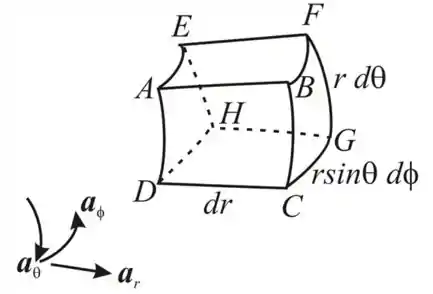
Um volume diferencial em coordenadas esféricas é mostrado na Figura 3.8. Para o elemento de volume, relacione os itens da coluna da esquerda com os da coluna direita.
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Passo 1
Falaaa moçada, olha que belezinha, bora começar com o diagrama ???
Partiuuuu
Passo 2
Pela figura acima
Passo 3
Forme a figura
Passo 4
Forme a figura
Passo 5
Forme a figura acima
Passo 6
Forme a figura acima
Passo 7
Forme a figura acima
Passo 3
Logo podemos concluir partindo das explicações que a combinação ficará da seguinte maneira,
- (v)
- (vi)
- (iv)
- (iii)
- (i)
- (ii)
Resposta
Vide o passo a passo.