Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Munson, Mecânica dos Fluidos- Ed: 4º - Capítulo 5.Problemas - Ex. 30

Água escoa na contração com seções transversais circulares esboçada na fig P 5.30 . A velocidade na seção ( 1 ) é uniforme e igual a 7,6   m / s e a pressão nesta seção é 5,17   b a r . A água é descarregada da contração pela seção ( 2 ) com velocidade de 30,5   m / s . Determine a componente axial da força de reação exercida pela contração sobre o escoamento. Determine a componente axial da força necessária para imobilizar a contração

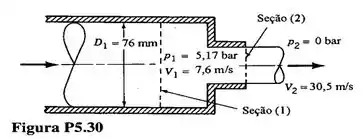
Passo 1

E aí, galerinha! Oia nós aqui de novo!

Mais um exercício de conservação de massa!

Vamos começar fazendo um esboço, delimitando o volume de controle e destacando as forças atuantes nesse sistema...

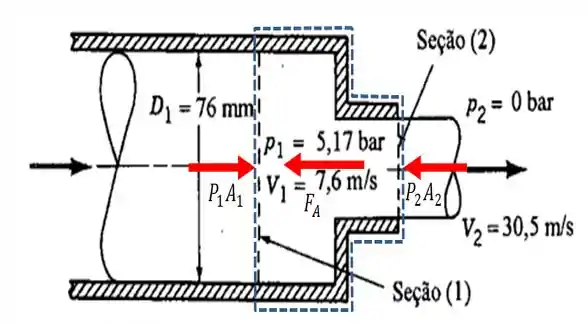
Dessa forma, aplicando a fórmula da conservação de massa ao longo do volume de controle, temos que...

∂ ∂ t ∫ C V ρ d ⩝ + ∫ C S ρ V → n ^ d A = 0

E quando a gente tá falando em volume de controle e conservação de massa... Considerando o nosso escoamento como incompressível, temos que a vazão vai ser a mesma ao longo de todo o fluxo do líquido...

v a z ã o   [ Q ] :   ( ' ' E u   s o u   i m u t á v e l ,   t á   g a l e r a   ? " )

Passo 2

Assim, aplicando o somatório das forças em relação à x , temos que...

∑ F x = 0

- V 1 ρ V 1 A 1 + V 2 ρ V 2 A 2 = P 1 A 1 - F A - P 2 A 2

Pela equação de conservação de massa, temos que...

m ˙ = ρ V 1 A 1 = ρ V 2 A 2

Então, a equação anterior fica assim...

m ˙ V 2 - V 1 = P 1 A 1 - F A - P 2 A 2

Isolando F A :

F A = P 1 A 1 - P 2 A 2 - m ˙ V 2 - V 1

F A = P 1 π d 1 2 4 - P 2 π d 2 2 4 - ρ V 1 A 1 V 2 - V 1

E substituindo os valore numéricos, obtemos que...

F A = P 1 π d 1 2 4 - P 2 π d 2 2 4 - ρ V 1 A 1 V 2 - V 1

F A = ( 5,17 ⋅ 100000 ) π 0,076 2 4 - ( 1000 ) ( 7,6 ) π 0,076 2 4 30,5 - 7,6

F A = 1555,82425   N

Resposta

F A = 1555,82425   N