Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 132

Os alimentos congelados podem ser descongelados simplesmente deixando-os sobre o balcão, mas isso é muito demorado. O processo pode ser consideravelmente acelerado para itens planos, como bifes, colocando-os sobre uma peça grande de metal altamente condutor, chamada placa de degelo, que serve como aleta. O aumento da superfície aumenta a transferência de calor e, portanto, reduz o tempo de degelo.

Considere dois bifes congelados de 1,5   c m de espessura a - 18 ℃ que parece um objeto circular de 15   c m de diâmetro, quando colocados um ao lado do outro. Os bifes são colocados na placa de degelo circular de alumínio anodizado de preto de 1   c m de espessura ( k = 237   W / m . K ,     α = 97,1 × 10 - 6 m 2 / s e ε = 0,9 ) cujo diâmetro externo é 30   c m . As propriedades da carne congelada são ρ = 970 k g / m ³ ,   C p = 1,55   k J / k g K ,   k = 1,40   W / m . K ,   α = 0,93 × 10 - 6   m ² / s ,   ε = 0,95 , e o calor de fusão é h f u s = 187   k J / k g . Os bifes podem ser considerados descongelados quando sua temperatura média for 0 ℃ e todo o gelo dos bifes derreter. Inicialmente, a placa de degelo está na temperatura ambiente de 20 ℃ , e a superfície de madeira em que é colocada pode ser tratada como isolamento. Além disso, as superfícies envolventes podem ser consideradas na mesma temperatura que o ar ambiente, bem como o coeficiente de transferência de calor por convecção para todas as superfícies expostas pode ser considerado 12   W / m ² K . A transferência de calor a partir das superfícies laterais da placa de degelo e dos bifes pode ser desprezada. Pressupondo uma condução de calor unidimensional em ambos os bifes e na placa de degelo, e usando método explícito de diferenças finitas, determine quanto tempo será necessário para descongelar os bifes. Use quatro pontos nodais com espaçamento de ∆ x = 0,5   c m para os bifes e 3 nós com espaçamento nodal ∆ r = 3,75   c m para a porção exposta da placa de degelo. Além disso, use passo de tempo ∆ t = 5 s . Dica: Em primeiro lugar, determine o valor total da transferência de calor necessária para descongelar os bifes e, então, determine o tempo necessário para transferir esse calor.

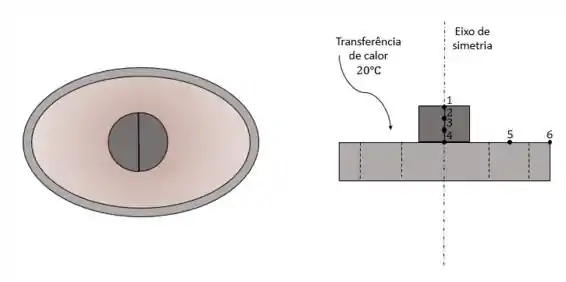
Figura representativa das vistas superior e frontal do esquema proposto

Passo 1

Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:

  • A transferência de calor em ambos os bifes e na placa de degelo é unidimensional, e a transferência de calor nas superfícies laterais é desprezível.
  • A transferência de calor na superfície inferior da placa é desprezível.
  • As propriedades térmicas, os coeficientes de transferência de calor, as temperaturas do ar ambiente e da superfície se mantém constantes durante o descongelamento.
  • A resistência térmica de contato entre os bifes e a placa de degelo é desprezível.
  • O resfriamento evaporativo dos bifes é insignificante.
  • O calor transferido para o prato é transferido direto para os bifes, pois a quantidade de calor total transferida para os bifes é muito maior que a quantidade de calor armazenada pelo prato.

De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.

Passo 2

Temos 6 temperaturas desconhecidas nesse problema, então precisaremos de 6 equações para resolvê-lo. Sabendo que os nós 2 e 3 são nós interiores de uma parede plana, para eles usaremos a formulação geral explícita de diferenças finitas, expressa da seguinte maneira:

T m - 1 i - 2 T m i + T m + 1 i + e ˙ m i ∆ x 2 k =   T m i + 1 -   T m i τ   →   T m i + 1 =   τ T m - 1 i +   T m + 1 i + 1 - 2 τ T m i

Para os outros nós, iremos utilizar a abordagem do balanço de energia, tomando as transferências de calor de todas as direções possíveis em relação ao nó em questão:

Nó 1:

h T ∞ -   T 1 i + ε b i f e σ T ∞ + 273 4 - T 1 i + 273 4 + k b i f e T 2 i -   T 1 i ∆ x =   ρ C p b i f e ∆ x 2 T 1 i + 1 -   T 1 i ∆ t

Nó 2 (interior):

T 2 i + 1 =   τ b i f e T 1 i +   T 3 i + 1 - 2 τ b i f e T 2 i

Nó 3 (interior):

T 3 i + 1 =   τ b i f e T 2 i +   T 4 i + 1 - 2 τ b i f e T 3 i

Nó 4:

π r 45 2 -   r 4 2 h T ∞ -   T 4 i + ε p r a t o σ T ∞ + 273 4 - T 4 i + 273 4 + k b i f e π r 4 2 T 3 i - T 4 i ∆ x + k p r a t o 2 π r 45 δ T 5 i -   T 4 i ∆ r = ρ C p b i f e π r 4 2 ∆ x 2 + ρ C p p r a t o π r 45 2 δ T 4 i + 1 -   T 4 i ∆ t

Nó 5:

2 π r 5 ∆ r h T ∞ - T 5 i + ε p r a t o σ T ∞ + 273 4 - T 5 i + 273 4 + k p r a t o 2 π r 56 δ T 6 i -   T 5 i ∆ r = ρ C p p r a t o π r 5 2 δ T 5 i + 1 -   T 5 i ∆ t  

Nó 6:

2 π r 56 +   r 6 2 ∆ r 2 h T ∞ - T 6 i + ε p r a t o σ T ∞ + 273 4 - T 6 i + 273 4 + k p r a t o 2 π r 56 δ T 5 i -   T 6 i ∆ r = ρ C p p r a t o 2 π r 56 + r 6 2 ∆ r 2 δ T 6 i + 1 -   T 6 i ∆ t  

Onde τ =   α ∆ t / ∆ x ² .

Passo 3

Os raios necessários à resolução podem ser calculados:

r 4 = 0,075 m

r 5 = 0,1125 m

r 6 = 0,1 5 m

r 4 5 = 0,075 + 0,1125 2 m

r 56 = 0 , 1125 + 0,1 5 2 m

Lembrando que r 4 é considerado na parede do bife, mantendo o espaçamento nodal sobre o prato.

Passo 4

A massa dos bifes também é necessária, sendo calculada da seguinte forma:

m b i f e =   ρ V =   970   k g / m ³ π 0,075 ² ( 0,015 ) =   0,257   k g

E agora é possível calcular a quantidade de calor total necessária para descongelar os bifes, da seguinte forma:

Q t o t a l ,   b i f e = Q s e n s í v e l + Q l a t e n t e =   m C p ∆ t b i f e + m h f u s b i f e =   0,257   k g 1,55   k J / k g K 0 - ( - 18 ) + 0,257   k g 187   k J / k g = 55,2   k J

E, sabendo que a quantidade de calor transferida para o bife é uma soma entre a quantidade de calor proveniente da superfície superior e da quantidade transferida indiretamente pelo prato, temos que:

Q b i f e i = 2 π r 5 ∆ r h T ∞ - T 5 i + ε p r a t o σ T ∞ + 273 4 - T 5 i + 273 4 + 2 π r 56 +   r 6 2 ∆ r 2 h T ∞ - T 6 i + ε p r a t o σ T ∞ + 273 4 - T 6 i + 273 4 + π r 45 2 -   r 4 2 h T ∞ -   T 4 i + ε p r a t o σ T ∞ + 273 4 - T 4 i + 273 4 + π r 1 h T ∞ -   T 1 i + ε b i f e σ T ∞ + 273 4 - T 1 i + 273 4

Então, a obtenção do tempo necessário para descongelar os bifes se dá pela determinação da quantidade de transferência de calor de cada etapa, e somada até obtermos 55,2   k J . Em outras palavras, o resultado da expressão encontrada acima é o equivalente a essa transferência em apenas um passo de tempo, então multiplica-se por um valor N para chegarmos aos 55,2   k J pretendidos.

Substituindo-se os valores que a questão fornece e os que calculamos previamente, observamos que o valor obtido deve ser multiplicado por 44 para chegarmos à quantidade necessária de calor para descongelar o bife. Logo, procede-se assim:

∆ t d e s c o n g e l a m e n t o = N ∆ t = 44 5 s = 220 s

Resposta

∆ t d e s c o n g e l a m e n t o = 220 s

Ver Outros Exercícios desse livro