O bocal horizontal mostrado na fig descarrega água na atmosfera. O componente da direção da força necessária para imobilizar o bocal, , é igual a quando o manômetro indica pressão relativa de . Determine, nestas condições, a vazão em volume e o componente da direção da força necessária para imobilizar o bocal. Desconsidere o atrito no escoamento...
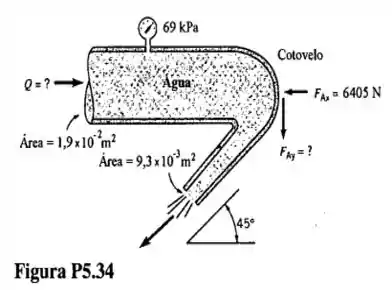
Passo 1
E aí, galerinha! Oia nós aqui de novo!
Mais um exercício de conservação de massa!
Dessa forma, aplicando a fórmula da conservação de massa ao longo do volume de controle, temos que...
E quando a gente tá falando em volume de controle e conservação de massa... Considerando o nosso escoamento como incompressível, temos que a vazão vai ser a mesma ao longo de todo o fluxo do líquido...
Passo 2
Assim, aplicando a equação de força para os componentes em , temos que...
Como pela figura, podemos ver que...
Então, ficamos com:
Passo 3
Agora, como pela conservação de massa, temos que:
Ou reescrevendo...
Isolando e substituindo os valores numéricos podemos obter a velocidade na primeira seção:
Passo 4
E para achar a pressão na seção (1), vamos usar a equação de Bernoulli para o fluido entre as seções (1) e (2):
Isolando e substituindo os valores numéricos...
Como , então:
Passo 5
Aí então fica de boas! Com base na equação do final do :
Passo 6
Para achar a componente , vamos usar a mesma equação de força.... Dando uma olhada na figura, temos que:
Pronto! Encontramos nossas respostas!