Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Munson, Mecânica dos Fluidos- Ed: 4º - Capítulo 5.Problemas - Ex. 15

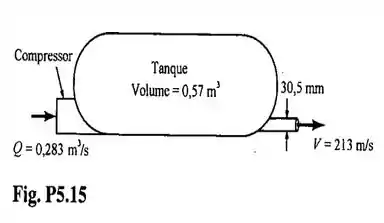
O compressor indicado na figura P 5.15 é alimentado com 0,283   m 3 / s de ar na condição padrão. O ar é descarregado no tanque através de uma tubulação que apresenta diâmetro igual a 30,5   m m . A velocidade e a massa específica de ar que escoa no tubo de descarga são iguais a 213   m / s e 1,80   k g / m 3

(a) Determine a taxa de variação da massa de ar contida no tanque em k g / s

(b) Determine a taxa média de variação da massa específica do ar contida no tanque

Passo 1

Bom! Mais uma aí, galera!

Mesmo esquema, galera! Mais um exercício sobre volume de controle!

Vimos na teoria que para um volume de controle, o que entra tem que ser igual ao que sai.

Assim, usando a fórmula do fluxo de massa...

d d t M s i s t e m a = m ˙ e n t r a d a - m ˙ s a í d a

d d t M s i s t e m a = ρ e n t r a d a Q e n t r a d a - ρ s a í d a Q s a í d a

d d t M s i s t e m a = ρ e n t r a d a Q e n t r a d a - ρ s a í d a A s a í d a V s a í d a

Passo 2

Como...

ρ e n t r a d a = > ρ a r   n a s   c o n d i ç õ e s   p a d r ã o = 1,2754   k g / m 3

Q e n t r a d a = 0,283   m 3 / s

ρ s a í d a = 1,8   k g / m 3

Então, pra achar a taxa de variação de massa... Basta substituir os valores numéricos...

d d t M s i s t e m a = ρ e n t r a d a Q e n t r a d a - ρ s a í d a A s a í d a V s a í d a

d d t M s i s t e m a = 1,2754 ⋅ 0,283 - 1,8 ⋅ π 4 0,0305 2 ⋅ 213

d d t M s i s t e m a = 0,081   k g / s

Passo 3

b) Encontrada a taxa de variação de massa, para achar a taxa média de variação da massa específica do ar contida no tanque, basta usar a relação abaixo...

d d t M s i s t e m a = d d t ρ V s i s t e m a

d d t M s i s t e m a = V s i s t e m a d d t ρ

Isolando a taxa de variação da massa específica e substituindo os valores numéricos...

d d t ρ = d d t M s i s t e m a V s i s t e m a

Uma vez que V s i s t e m a = V t a n q u e = 0,57   m 3 :

d d t ρ = d d t M s i s t e m a V s i s t e m a

d d t ρ = 0,081   k g / s 0,57   m 3

d d t ρ = 0,1421   k g / m 3 ⋅ s

Resposta

a)

d d t M s i s t e m a = 0,081   k g / s

b)

d d t ρ = 0,1421   k g / m 3 ⋅ s