Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 69

Considere uma barra longa de concreto k = 0,6 W m ∙ K , σ s = 0,7 de seção transversal triangular cuja superfície exposta é submetida a fluxo de calor solar q ˙ s = 800   W / m 2 e convecção e radiação para o meio ambiente a 25   ° C com coeficiente combinado de transferência de calor de   30 W m 2 ∙ K . A seção vertical da barra de 2   m de altura é submetida à convecção para água a 15   ° C , com coeficiente de transferência de calor de 150 W m 2 ∙ K . A transferência de calor através da base de 2   m   de comprimento é considerada desprezível. Usando o método das diferenças finitas com tamanho de malha de ∆ x = ∆ y = 1   m , e considerando a transferência de calor permanente bidimensional, determine a temperatura nos lados superior, inferior e do meio da superfície da barra exposta.

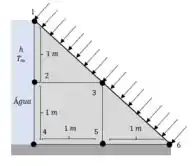
Passo 1

Vamos lá...do enunciado temos os seguintes dados:

l = 1   m ;   k = 0,6 W m ∙ K ; σ s = 0,7 ;   q ˙ s = 800 W m 2 ; h o = 30 W m 2 ∙ K   ; h i = 150 W m 2 ∙ K  

T i = 15 ° C ; T o = 25 ° C

Usaremos nesse exercício nossa equação para malha quadrada, dada abaixo:

T e s q + T s u p + T d i r + T i n f - 4 T n ó = 0

Passo 2

Agora basta formularmos as equações de diferença finita para cada nó...

N ó   1 :

h i l 2   T i - T 1 + k l 2 T 2 - T 1 l + l 2 sen ⁡ 45 σ s q ˙ s + h o T o - T 1 = 0

N ó   2 :

h i l 2   T i - T 1 + k l 2 T 1 - T 2 l + k l T 3 - T 2 l = 0

N ó   3 :

k l T 2 - T 3 l + k l T 5 - T 3 l + l 2 sen ⁡ 45 σ s q ˙ s + h o T o - T 3 = 0

N ó   4 :

h i l 2   T i - T 4 + k l 2 T 2 - T 4 l + l 2 T 5 - T 4 l = 0

N ó   5 :

T 4 + 2 T 3 + T 6 - 4 T 5 = 0

N ó   6 :

k l 2 T 5 - T 6 l + l 2 sen ⁡ 45 σ s q ˙ s + h o T o - T 6 = 0

Resposta

Resolvendo as 6 equações simultaneamente, as temperaturas serão:

T 1 = T s u p = 21,3 ° C

T 2 = 15,1 ° C

T 3 = T m e i o = 43,2 ° C

T 4 = 15,1 ° C

T 5 = 36,3 ° C

T 6 = T i n f = 43,6 ° C

Ver Outros Exercícios desse livro