Considere uma condução de calor permanente unidimensional em uma aleta do tipo pino com diâmetro constante e condutividade térmica constante. A aleta perde calor por convecção para o ar ambiente a com coeficiente de transferência de calor e por radiação para as superfícies ao redor na temperatura de . A rede nodal da aleta consiste dos nós 0 (na base), 1 (no meio) e 2 (na ponta da aleta), com espaçamento nodal uniforme de . Usando a abordagem do balanço de energia, obtenha a formulação de diferenças finitas do problema para determinar e para o caso de temperatura especificada na base da aleta e transferência de calor desprezível na ponta da aleta. Todas as temperaturas estão em .
Passo 1
Eai pessoal, tudo certo?
Bom, vamos representar esse problema através de um desenho:
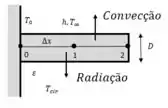
Note que no enunciado nos diz que é uma aleta que sofre convecção e radiação, logo precisamos nos atentar quando formos realizar o balanço de energia.
Passo 2
Para encontrarmos a formulação para a temperatura , podemos aplicar o balanço de energia no ponto central. E não vamos nos esquecer de considerar a radiação, certo?
Lembrando...no enunciado diz que a temperatura está em , logo precisamos somar para deixar em , pois a temperatura na radiação é considerada nessa escala!
Logo, temos...
Continuando para temperatura 2...
Onde...
Resposta
Ei, a resposta está no passo a passo :)