Considere a condução de calor permanente unidimensional em uma parede plana composta que consiste de duas camadas, e , em perfeito contato na interface. A parede não envolve geração de calor. A rede nodal do meio consiste dos nós 0, 1 (na interface) e 2, com espaçamento nodal uniforme de . Usando a abordagem do balanço de energia, obtenha a formulação de diferenças finitas desse problema para o caso de isolamento no contorno esquerdo (nó 0) e de radiação no contorno direito (nó 2), com emissividade e temperatura das superfícies envolventes de .
Passo 1
Vamos lá pessoal, primeira coisa que podemos fazer para nos ajudar a ter uma visualização é um esboço do problema...
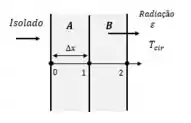
Prontinho, agora basta aplicarmos o balanço de energia.
Passo 2
Aplicando o balanço de energia para o lado esquerdo no nó 0, onde o mesmo se encontra isolado:
Agora para aplicarmos o balanço de energia entre a interface e temos que considerar os materiais que são diferentes, ou seja, terá um e um :
Por fim aplicando no lado direito em contato com o ambiente temos...
Resposta
Ei, a resposta está no passo a passo :)