Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 70

Considere uma longa barra sólida de condutividade térmica k = 5 W m ∙ K e a seção transversal dada na Fig. P5–70. A superfície superior da barra é mantida a 50   ° C , enquanto a inferior é mantida a 120   ° C . A superfície esquerda é isolada, e as três restantes são submetidas à convecção para o ar ambiente a T ∞ , com coeficiente de transferência de calor   h = 40 W m 2 ∙ K . Usando o método de diferenças finitas com tamanho da malha de   ∆ x = ∆ y = 10   c m , ( a ) obtenha a formulação de diferenças finitas para este problema de transferência de calor permanente bidimensional e ( b ) determine as temperaturas nodais desconhecidas resolvendo as equações.

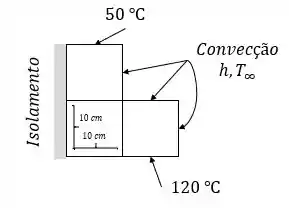
Passo 1

Do enunciado temos os seguintes dados abaixo:

l = 0,1   m ; k = 5 W m ∙ K ; h = 40 W m 2 ∙ K ; T ∞ = 25 ℃ ;   ∆ x = ∆ y = l = 10   c m

Note que a temperatura inferior e superior está indicada na imagem, logo gerando nossa malha, precisamos encontrar as temperaturas nos pontos indicados na figura:

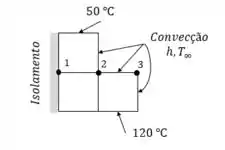
O nó 1 pode ser tratado como nó interior por causa do isolamento, logo...

T e s q + T s u p + T d i r + T i n f - 4 T n ó = 0

Passo 2

Agora podemos aplicar o balanço de energia em cada nó, na qual ficará assim:

N ó   1 :

50 + 120 + 2 T 2 - 4 T 1 = 0

N ó   2 :

h l T ∞ - T 2 + k l 2 50 - T 2 l + k l 2 T 3 - T 2 l + k l T 1 - T 2 l + k l 120 - T 2 l = 0

N ó   3 :

h l T ∞ - T 3 + k l 2 T 2 - T 3 l + k l 2 120 - T 3 l = 0

Resposta

Resolvendo as questões simultaneamente, temos as seguintes temperaturas:

T 1 = 78,8   ℃

T 2 = 72,7 ℃

T 3 = 64,6 ℃

Ver Outros Exercícios desse livro