Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 93

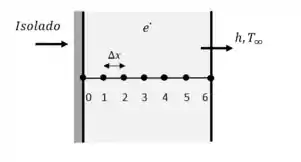
Considere uma placa de urânio de espessura L = 9   c m , condutividade térmica k = 28 W m ∙ K   e difusividade térmica α = 12,5 × 10 - 6 m 2 s inicialmente a temperatura uniforme de 100   ° C . O calor é gerado de modo uniforme na chapa a uma taxa constante de e ˙ = 10 6 W m 3 . No instante t = 0 o lado esquerdo da chapa é isolado, enquanto o outro lado está́ sujeito à convecção para o ambiente a   T ∞ = 20 ° C , com coeficiente de transferência de calor   h = 35 W m 2 ∙ K . Usando abordagem explicita de diferenças finitas com espaçamento nodal uniforme de ∆ x = 1,5   c m , determine ( a ) a distribuição de temperatura na chapa após 5   m i n e ( b ) quanto tempo demora para as condições permanentes na chapa serem alcançadas.

Passo 1

A partir do enunciado temos os seguintes dados:

L = 9   c m ;   k = 28 W m ∙ K ;   α = 12,5 × 10 - 6 m 2 s ;   e ˙ = 10 6 W m 3 ;  

T ∞ = 20 ° C ;   h = 35 W m 2 ∙ K ;   ∆ x = 1,5   c m

Note que precisamos encontrar quantos nós será necessário para resolvermos os problemas, e podemos encontrar a partir da formula abaixo:

M = L ∆ x + 1 = 0,09 0,015 + 1 = 7

Temos que o lado esquerdo da chapa está isolado e o lado direito da chapa está sujeito a convecção, logo...

Passo 2

Para os nós interiores, podemos utilizar a formulação geral do método explícito abaixo:

T m - 1 i - 2 T m i + T m + 1 i + e ˙ m i ∆ x 2 k = T m i + 1 - T m i τ

T m i + 1 = τ T m - 1 i + T m + 1 i + 1 - 2 τ T m i + τ e ˙ m i ∆ x 2 k

Passo 3

Logo, obtendo a equação para cada nó...

N ó   0 :

T 0 i + 1 = τ T 1 i + T 1 i + 1 - 2 τ T 0 i + τ e ˙ 0 ∆ x 2 k

N ó   1 :

T 1 i + 1 = τ T 0 i + T 2 i + 1 - 2 τ T 1 i + τ e ˙ 0 ∆ x 2 k

N ó   2 :

T 2 i + 1 = τ T 1 i + T 3 i + 1 - 2 τ T 2 i + τ e ˙ 0 ∆ x 2 k

N ó   3 :

T 3 i + 1 = τ T 2 i + T 4 i + 1 - 2 τ T 3 i + τ e ˙ 0 ∆ x 2 k

N ó   4 :

T 4 i + 1 = τ T 3 i + T 5 i + 1 - 2 τ T 4 i + τ e ˙ 0 ∆ x 2 k

N ó   5 :

T 5 i + 1 = τ T 4 i + T 6 i + 1 - 2 τ T 5 i + τ e ˙ 0 ∆ x 2 k

N ó   6 :

h T ∞ - T 6 i + k T 5 i - T 6 i ∆ x + e ˙ 0 ∆ x 2 = ρ ∆ x 2 c p T 6 i + 1 - T 6 i ∆ t

Passo 4

Aplicando o critério de estabilidade para obtermos o passo de tempo ∆ t :

1 - 2 τ - 2 τ h ∆ x k ≥ 0

τ ≤ 1 2 1 + h ∆ x k

Note que...

τ = α ∆ t ∆ x 2

∆ t ≤ ∆ x 2 2 α 1 + h ∆ x k

Logo temos:

∆ t ≤ 0,015   m 2 2 12,5 × 10 - 6 m 2 s 1 + 35 W m 2 ∙ K 0,015   m 28 W m ∙ K = 8,8   s

Portanto deve ser escolhido um passo de tempo menor que 8,8   s . Sendo assim vamos escolher um passo de tempo de ∆ t = 7,5   s .

τ = α ∆ t ∆ x 2 = 12,5 × 10 - 6 m 2 s 7,5   s 0,015   m 2 = 0,4167

Passo 5

Por fim, para encontrarmos a distribuição de temperatura após 5   m i n :

P a s s o s   d e   t e m p o = 5 × 60 7,5 = 40   P a s s o s   d e   t e m p o

Após 5   m i n , temos:

T 0 = 229,9 ° C

T 1 = 229,7 ° C

T 2 = 229,0 ° C

T 3 = 227,7 ° C

T 4 = 225,8 ° C

T 5 = 223,3 ° C

T 6 = 220 ° C

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro