Determine o valor R de verão e o fator U da parede de moldura de madeira que é construída com vigas de madeira de com distância centro a centro de 400 mm. A cavidade de 140 mm de largura entre as vigas é preenchida com isolamento de fibra mineral (lã de rocha). O interior é acabado com placas de gesso de 13 mm, e as paredes externas são acabadas com placas de fibra de madeira (compensado) e tábuas de madeiras chanfradas de . A cavidade isolada constitui 80% da área de transmissão de calor, enquanto vigas, guias e placas constituem 20%.

Agoora sim galeraaa!!

Vamos começar com os cálculos!!

No livro nós achamos uma situação bem parecida com essa e, por isso, vou trazer o desenho aqui para vocês visualizarem melhor a situação, ok?

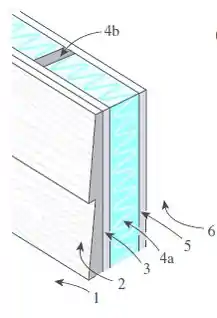
E agora?

Agora nós vamos construir uma tabela com os valores de R apresentadas na Tabela 3-8.

A tabela nos fornece todos os dados, no entanto, o isolamento de lã de rocha usado aqui é de 140 mm, mas a tabela nos fornece o valor de R apenas para uma espessura de 25 mm.

A tabela nos diz que:

Uma regra simples de três nos dá que:

Prestem atenção aqui!! A lã de rocha está presente somente entre as vigas, enquanto os valores de R para as vigas de madeira nós colocamos somente na coluna “nas vigas”. Os restantes dos valores estão presentes em ambas as colunas (Tabelinha abaixo )!

Beleza! Já temos então todas as resistências térmicas unitária, né?

Com isso nós podemos achar a resistência térmica total para cada seção. Como? Simples!! Nós vamos somar tudinho!!

Com a resistência térmica total nós podemos achar o fator U para cada seção pela fórmula:

Para fazer uma tabela foda mesmo vamos terminar adicionando a fração da área é constituída por cada uma da seção!

Preparados?? Então bora lá !!

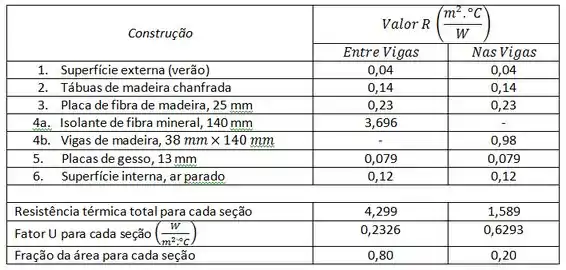
E aí? Achamos o que precisávamos ou não?

Que nada né!!