Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 73
Ar entra em um bocal convergente-divergente de um túnel de vento supersônico a 1 MPa e 300 K com velocidade baixa. Se uma onda de choque normal ocorrer no plano de saída
do bocal a Ma = 2, determine a pressão, temperatura, o número de Mach, a velocidade e a pressão de estagnação após a onda de choque.
Passo 1
Vamos lá! O problema quer que a gente encontre a pressão, temperatura, o número de Mach, a velocidade e a pressão de estagnação após a onda de choque.
Uhooow, um monte de coisa!!
E como a gente faz isso?!
Calminha, primeiro vamos visualizar:
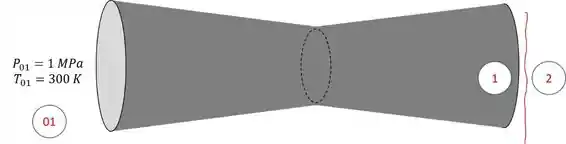
Você pode notar que na entrada do bocal eu já coloquei ali o , isso porque o problema diz que a velocidade com que o ar entra no bocal é baixa, se a gente considerar essa velocidade nula podemos dizer que a pressão e a temperatura nesse ponto é de estagnação, não podemos?!
Passo 2
Podemos começar calculando as propriedades no ponto :
Substituindo e calculando:
Agora podemos achar:
Calculando:
Passo 3
Agora a gente vai dar uma corridinha atrás do livro na tabela e a gente vai ver que pra temos:
Aweee, primeira resposta!!
Passo 4
Com as relações do passo 2 podemos achar a pressão de estagnação, a pressão e a temperatura após a onda de choque:
Para
Agora :
Para :
:
Para
Agora só falta a velocidade!
Lembra dessa equação aqui:
E essa:
Juntando elas podemos achar :
é tabelado, , mas sabendo que:
Logo:
A gente fez isso pra ter a resposta final em !!
Acabooooou!!!