Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 57
Ar escoa isentropicamente através de um bocal convergentedivergente conectado a um grande tanque no qual a pressão é 1,73 MPa e a temperatura é 280 K. O bocal está operando nas condições de projeto para as quais a pressão na saída do bocal, pe, é igual à pressão atmosférica local, pa. A área de saída do bocal é Ae = 1016 mm². Calcule a vazão através do bocal. Trace um gráfico da vazão mássica para um aumento progressivo da temperatura do tanque até 1110 K (todas as pressões permanecendo as mesmas). Explique esse resultado (por exemplo, compare as vazões mássicas a 280 K e 1110 K).
Passo 1
Oi pessoal, tudo bem ?
Consideremos:
As propriedades do ar são provenientes da Tabela A.6.
Devemos lembrar que a vazão mássica através do bocal é dada por:
E até agora, só temos o valor da área de saída do bocal. Então devemos encontrar a velocidade de saída e a massa específica.
Passo 2
Afim de descobrir a velocidade de saída do bocal, sabemos que:
A razão da pressão estática com a pressão total pode ser encontrada através de :
A pressão no tanque é a pressão de estagnação, a pressão de saída foi informada que é igual a pressão atmosférica, e para o ar-padrão o k=1,4. Então, fazendo as devidas manipulações e substituindo os valores, temos:
A temperatura de saída é informada por:
Então a velocidade de saída do ar do bocal é:
Passo 3
O pode ser encontrado pela relação:
Então, a vazão mássica é:
Portanto:
Resposta
Fazendo variar a temperatura de estagnação, ocorrerá uma variação em cadeia, até a variação da vazão mássica. Com o auxílio do Excel, é possível fazer essa análise, como mostra a tabela a seguir:
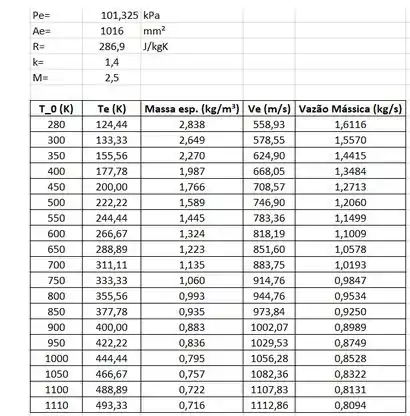
Assim, o gráfico fica da seguinte forma:
