Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 198
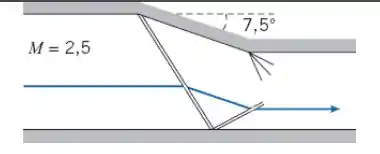
Ar escoa isentropicamente com M = 2,5 em um duto. Existe uma contração de 7,5° que causa um choque oblíquo, que reflete sobre uma parede, gerando uma segunda onda de choque oblíquo. Esse segundo choque é necessário, de modo que o fluxo acaba fluindo paralelo às paredes do canal após os dois choques. Encontre o número de Mach e a pressão na contração e a jusante da contração. (Note que a quina convexa causará ondas de expansão para redirecionar o fluxo ao longo da parede superior.)
Passo 1
Fala aí galera, bora pra mais uma questão de Mecânica dos fluidos para tirarmos aquele notão na prova. Para o primeiro choque oblíquo (1 a 2), precisamos encontrar a partir da equação abaixo, temos:
Escolhemos iterando ou usando a Busca de meta para segmentar (abaixo) para igualar o dado . Logo, usando a função interna theta
Então pode ser encontrado a partir da equação abaixo, temos:
E para , temos:
Então, a partir de , podemos encontrar . Fica assim:
Com isso, a pressão é dada por:
Passo 2
Repetimos a análise dos estados a para os estados a , para analisar o segundo choque oblíquo. Escolhemos para o iterando, temos que:
Então, podemos encontrar (normal ao segundo choque!), dado por:
Com isso, podemos encontrar :
Então, a partir de , podemos encontrar . Temos:
Por fim, podemos encontrar a pressão à jusante a partir de . Fica assim: