Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Munson, Mecânica dos Fluidos- Ed: 4º - Capítulo 4.Problemas - Ex. 40

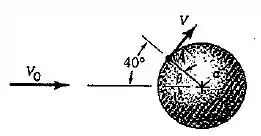
Faça um gráfico de a s , aceleração na direção da linha de corrente, e de a n , aceleração na direção normal à linha de corrente, em função de θ para o escoamento do problema anterior. Considere V 0 = 15 m s ,   0 ≤ θ ≤ 90 °   e   a = 30 ; 300   e   3000   m m . Repita o problema com V 0 = 1,5   m / s . A aceleração é máxima em que local do escoamento?

Passo 1

Falaaa pessoal, como vocês estão? Bom, bora pra mais uma questão que envolve programa computacional na sua resolução!

Lá do problema anterior e dessa situação em geral, a gente tem as seguintes igualdades pras componentes da aceleração e velocidade:

V = 3 2 V 0 sin ⁡ θ   m / s

a n = V 2 R = 3 2 V 0 sin ⁡ θ 2 a = 9 V 0 2 4 a sin 2 ⁡ θ

a s = V δ V δ s = 3 2 V 0 sin ⁡ θ 3 2 V 0 cos ⁡ θ 1 a = 9 V 0 2 4 a sin ⁡ θ cos ⁡ θ

Como já temos as duas componentes da aceleração, na direção e normal, podemos encontrar a magnitude dela:

a → = a n 2 + a s 2 1 / 2 = 9 V 0 2 4 a sin ⁡ θ

Disso a gente consegue tirar que:

a → m i n = 0   q u a n d o   θ = 0

a → m a x = 9 V 0 2 4 a   q u a n d o   θ = 90 °

Passo 2

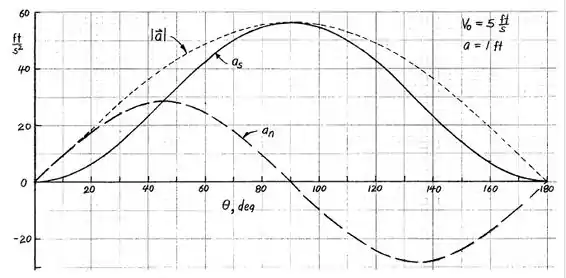
Os valores de a s ,   a n   e   a → , podem ser calculados no programa P4#40 para os valores trazidos no enunciado, e as ilustrações abaixo vão trazer esses dados pra gente. Detalhe que as unidades que eram metros aqui foram alteradas para pés:

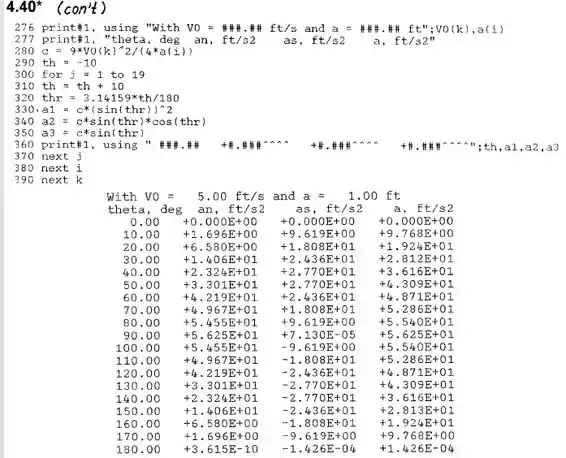
E então pode se montar o gráfico pedido na questão.

Resposta