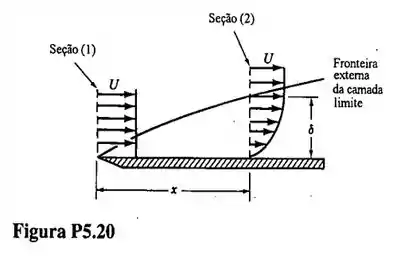
A fig mostra o escoamento de um fluido viscoso na região próximo a uma placa plana. Note que a velocidade de escoamento é nula na placa e aumenta continuamente até atingir um valor constante ao longe. Esta região que apresenta variação de velocidade é denominada "camada limite". O perfil de velocidade do escoamento pode ser considerado uniforme no bordo de ataque da placa e o valor da velocidade neste local é U. A velocidade também é constante e igual a na fronteira externa da camada limite. Se o perfil de velocidade longitudinal na seção (2) é dado por
Desenvolva uma expressão para calcular a vazão em volume na fronteira externa da camada limite delimitada entre o bordo de ataque e a seção transversal que apresenta espessura de camada limite igual a
Passo 1
Bom! Bora pra luta, meus queridos!
Vimos na teoria que para um volume de controle, o que entra tem que ser igual ao que sai.
Assim, baseado nesse princípio, aplicado ao fluxo através do volume de controle mostrado na figura que temos...
Passo 2
Só que para um fluxo incompressível, temos que...
Onde é a largura da placa. Sendo assim, ficamos com...