Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 1.Problemas - Ex. 72

In Fig. P2.72, gate AB is circular. Find the moment of the

hydrostatic force on this gate about axis A.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Desenhando as forças hidrostáticas agindo no portão

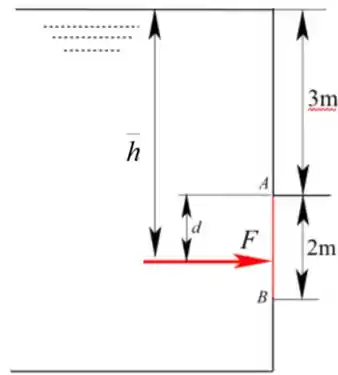
Passo 2

Calcule a força hidrostática que atua na porta circular.

F = γ h C G A F = ρ g h C G A

Aqui, é γ o peso específico da água, ρ é a densidade da água, g é a aceleração devido à gravidade, h C G centroide do portão da superfície livre da água, e A é a área do portão circular. Encontre a área do portão usando a seguinte equação:

A = π r 2

Aqui, r está o raio do portão.

Substitua 1   m por r .

A   = π ( 1   m ) 2   = 3.141   m 2

Passo 3

Calcule o centroide do portão a partir da superfície livre da água.

h C G   = 3   m + 1   m   = 4   m

Obtenha as propriedades da água à temperatura da 20 ∘ C Tabela A.1, "Propriedades da água" no livro didático. Densidade, ρ = 998   k g / m 3 Substituindo 998   k g / m 3 para ρ , 4   m para h C G , e 3.141   m 2 para A na equação.

F   = ρ g H c g A   = 998 × 9.81 × 4 × 3.141   = 123006.334   N

Passo 4

Calcule a altura do centro da pressão através da qual a força atua.

h ‾ = I x x h C G A + h C G

Aqui, I x x é o momento de inércia sobre o eixo x x . Encontre o momento de inércia usando a seguinte equação:

I x x = π r 4 4

Substitua 1   m r .

I x x   = π 4 ( 1   m ) 4   = 0.7854   m 4

Substitua 0.7854   m 4 por I x x , 4   m por h C G , e 3.1416   m 2 por A na equação.

h ‾   = I x x h C G A + h C G   = 0.7854 4 × 3.1416 + 4   = 4.0625   m

Passo 5

Encontre o momento da força hidrostática sobre o ponto A .

M   = F × d   = F × ( h ‾ - 3 )

Aqui, d é a altura da força hidrostática ao ponto A . Substituto 123006.334   N por F e 4.0625   m para d

M = 123006.334 × 4.0625 - 3   = 130694.229   N ∙   m

Portanto, o momento da força hidrostática sobre o eixo A é 130694.229   N ∙ m .

Resposta

M = 130694.229   N ∙ m