Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Munson, Mecânica dos Fluidos- Ed: 4º - Capítulo 4.Problemas - Ex. 41

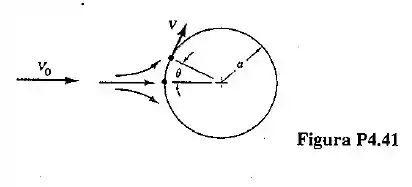
A Fig. P4.41 mostra o escoamento de um fluido em torno de um cilindro. A velocidade ao longe, V 0 , e a velocidade do escoamento pode ser aproximada por V = 2   V 0 sin ⁡ θ . Determine as componentes do vetor aceleração nas direções da linha de corrente e normal à linha de corrente na superfície do cilindro em função de V 0 ,   a   e   θ .

Passo 1

Falaaa pessoal, como vocês estão? Bom, bora pra mais uma questão desse assunto!

Pra componente normal nós vamos ter a relação abaixo e já vamos substituir as relações que o enunciado dá.

a n = V 2 R = 2   V 0 sin ⁡ θ 2 a = 4 V 0 2 a sin 2 ⁡ θ

Já para a outra componente, vamos ter:

a s = V δ V δ s = V δ V δ θ ∙ δ θ δ s

E nós temos que δ V δ θ = 2 V 0 c o s θ e δ θ δ s = 1 a . Logo, a gente vai chegar em:

a s = ( 2 V 0 sin ⁡ θ ) ( 2 V 0 cos ⁡ θ ) 1 a = 4 V 0 2 a sin ⁡ θ cos ⁡ θ  

Resposta

a n = 4 V 0 2 a sin 2 ⁡ θ

a s = 4 V 0 2 a sin ⁡ θ cos ⁡ θ