A figura mostra uma seringa hipodérmica que é utilizada para aplicar vacinas. Calcule a velocidade média do escoamento na agulha admitindo que a velocidade do êmbolo é constante e igual a e que a vazão em volume do vazamento é igual a da vazão de vacina na agulha. Os diâmetros internos da seringa e da agulha são respectivamente iguais a e .
Passo 1
E aí, galerinha! Simbora pra mais um exercício aí sobre volumes de controle!
Bora começar destacando o volume de controle pra ajudar a entender melhor o problema...
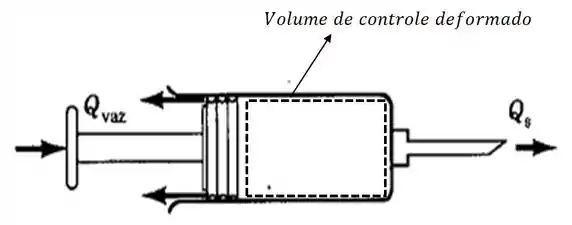
Então galera, esse é um exercício de conservação!
Dessa forma, aplicando a fórmula da conservação de massa ao longo do volume de controle, temos que...
E quando a gente tá falando em volume de controle e conservação de massa... Considerando o nosso escoamento como incompressível, temos que a vazão vai ser a mesma ao longo de todo o fluxo do líquido...
Passo 2
Dessa forma, com base no volume de controle deformado e usando o princípio de conservação de massa:
Uma vez que é constante... E que a vazão em volume do vazamento é igual a da vazão de vacina na agulha...
E temos também que...
Dessa forma, ficamos com...
Passo 3
Isolando a velocidade média do escoamento na agulha, ...
Como...
Então, ficamos com...