Um fluido escoa ao longo do eixo x com velocidade , onde x é medido em metros e t em segundos.
- Faça um gráfico da velocidade para .
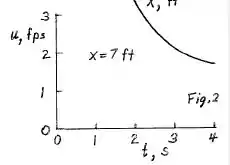
- Faça um gráfico da velocidade para .
- Determine os valores das acelerações local e convectiva.
- Mostre que a aceleração de qualquer partícula fluida do escoamento é nula.
- Explique porque as velocidades das partículas deste escoamento transitório permanecem constantes durante o movimento.
Passo 1
Falaaa pessoal, como vocês estão? Bom, bora pra mais uma questão desse assunto!
- Nesse item vamos simplesmente pegar a equação e substituir a variável de tempo pelos 3 segundos pedidos no enunciado.
- Aqui, em vez de substituir o tempo, substituiremos a posição para .
- Nós temos que a aceleração local se trata da própria que está ocorrendo naquele local, sendo:
- Sobre isso, nós temos por definição, que pra qualquer fluido com velocidade zerada, é válida a seguinte equação de aceleração:
- As partículas se movimentam mais em áreas de mais altas velocidades, mas pra qualquer local determinado, a velocidade diminui com o tempo. A gente viu nos itens anteriores que as acelerações locais e convectivas são iguais com sinais opostos, sempre resultando em uma aceleração zerada.
Agora é só substituir a variável de posição por . O gráfico a seguir demonstra isso só que com a unidade de pés.
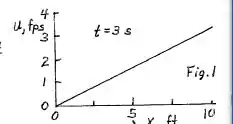
Agora é só substituir a variável de tempo por . O gráfico a seguir demonstra isso só que com a unidade de pés:
Passo 2
A aceleração convectiva é a própria, só que agora devido ao movimento em relação ao fluxo, sendo:
No item anterior, nós já determinamos o valor dessas duas parcelas aí. Então fica:
Resposta
Ei, a resposta está no passo a passo :)