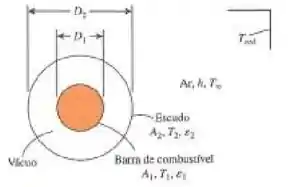
Uma longa barra cilíndrica de combustível de superfície negra de de diâmetro é protegida por uma superfície concêntrica à barra. O escudo tem diâmetro de , e sua superfície externa é exposta ao ar ao redor a com coeficiente de transferência de calor por convecção de . As superfícies interna e externa do escudo tem emissividade de , e o espaçamento entre a barra de combustível e o escudo é vácuo. Considerando que o escudo mantém uma temperatura uniforme de , determine a temperatura da superfície da barra de combustível.

Aplicando o balanço de energia na superfície externa, a taxa líquida de transferência de calor pode ser dada como:

Dados:

;

;

;

;

;

;

;

.

Temos:

Como a transferência de calor e o escudo centra radiação não mudam, a temperatura de superfície da barra de combustível é dada por:

Então:

Substituindo os dados: