Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 58
Óleo a 150°C escoa lentamente através de um tubo longo com parede delgada e diâmetro interno de 30 mm. O tubo está suspenso em uma sala na qual a temperatura do ar é de 20°C e o coeficiente de transferência de calor por convecção na superfície externa do tubo é de 11 W/(m2 · K). Estime a perda de calor por unidade de comprimento do tubo.
Passo 1
Vamo analisar o enunciado junto pra entender o que ele quer de você.
Temos um tubo por onde escoa um óleo a escoa lentamente, ao mesmo tempo que está exposto à convecção de ar, como demonstra o esquema ilustrativo abaixo, onde já estão demonstradas todas as grandezas que iremos usar ao longo da questão:
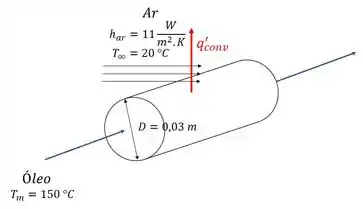
A questão quer que a gente calcule a taxa de calor por unidade de comprimento do tubo , a partir da equação:
Sendo a resistência térmica por unidade de comprimento.
Para calcular a resistência térmica, devemos analisar o circuito térmico para esse volume de controle, dado na figura abaixo:
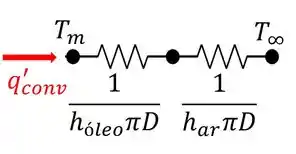
Ou seja, a transferência de calor se dá do seio do óleo até o ar externo ao tubo, sendo apenas as resistências à convecção no óleo e no ar significativas para o processo.
Dessa maneira, a resistência térmica é calculada da seguinte forma:
Pra gente resolver essa questão, vamo precisar procurar a condutividade térmica do óleo na Tabela A.5 (página 638) a uma temperatura , e, portanto, .
Agora a gente pode ir resolver a questão no próximo passo.
Passo 2
Para calcular a resistência térmica, precisamos antes calcular o coeficiente de transferência de calor a partir da equação:
Agora chega aqui mais perto, porque eu preciso te dar uns conceitos sobre convecção interna pra gente calcular esse coeficiente de transferência de calor.
Volta um pouco no enunciado. Ele diz que o escoamento de óleo é lento e que o tubo é longo. Isso significa dizer, em palavras um pouco mais difíceis pra tentar te distrair, é que o escoamento é laminar e completamente desenvolvido.
Ah, mas desse jeito a gente sabe bem fácil o número de Nusselt! Pra um escoamento laminar completamente desenvolvido . Sendo assim:
Pra finalizar a questão, vamos calcular o coeficiente de transferência de calor por unidade de comprimento:
Pronto, matamos a questão junto ;)
Resposta
O coeficiente de transferência de calor por unidade de comprimento é .