Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 24

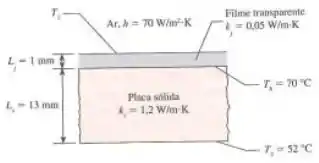
Uma película transparente será colada sobre a superfície superior de uma placa sólida dentro de uma câmara aquecida. Para colar adequadamente, a temperatura entre a cola, a película e placa sólida deverá ser mantida a 70 °C. O filme transparente tem espessura de 1 mm e condutividade térmica 0,05   W / m ⋅ K , enquanto a placa sólida tem 13 mm de espessura e condutividade térmica de 1,2   W / m ⋅ K . Dentro da câmara climatizada, o coeficiente de transferência de calor por convecção é 70   W / m 2 ⋅ K . Considerando que a superfície inferior da placa sólida é mantida a 52 °C, determine a temperatura no interior da câmara aquecida e a temperatura da superfície do filme transparente. Pressuponha uma resistência térmica de contato desprezível.

Passo 1

Nosso ponto de partida é colocar as hipóteses do nosso problema. São elas que possibilitam a sua solução!

Portanto, temos um problema de transferência de calor em regime permanente, unidimensional e condutividade térmica constante.

Podemos associar este problema a noção de resistências elétricas. O calor fluirá de dentro da câmara em direção a placa sólida. Portanto, temos 3 elementos no nosso circuito: uma resistência de convecção; uma resistência térmica de condução devido ao filme e uma resistência térmica de condução devido a placa sólida.

Podemos representar esta situação através da seguinte figura:

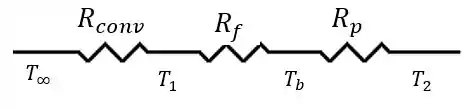
Calculando as resistências térmicas, temos:

R c o n v = 1 h = 1 70 = 0,0143   K ⋅ m 2 / W

R f = L f k f = 1 ⋅ 10 - 3 0,05 = 0,02   K ⋅ m 2 / W

R p = L p k p = 13 ⋅ 10 - 3 1,2 = 0,01083   K ⋅ m 2 / W

Agora, basta aplicarmos as fórmulas da condução para obtermos tanto a taxa de transferência de calor quanto a temperatura da superfície interna do vidro.

Passo 2

Vamos começar determinando a temperatura na superfície do filme. Para isto, precisamos utilizar a informação de que o fluxo de calor é constante por cada resistência térmica. Desta forma, comparando o fluxo entre as duas resistências de condução, temos:

T 1 - T b R f = T b - T 2 R p

Substituindo os valores das constantes e resolvendo para T 1 , que representa a temperatura na superfície interna do filme, temos:

T 1 = T b + R f R p ⋅ ( T b - T 2 )

T 1 = 70 + 0,02 0,01083 ⋅ 70 - 52

T 1 = 103,2   ° C

Passo 3

Para finalizarmos a questão, precisamos determinar a temperatura no interior da câmara. Para isto, precisamos realizar o mesmo procedimento da questão anterior, com exceção dos elementos analisados. Comparando o elemento de convecção e a resistência térmica da placa, temos:

T ∞ - T 1 R c o n v = T b - T 2 R p

T ∞ = T 1 + R c o n v R p ⋅ ( T b - T 2 )

T ∞ = 103,2 + 0,0143 0,01083 ⋅ 70 - 52

T ∞ = 127   ° C

Resposta

A temperatura na superfície interna do filme é:

T 1 = 103,2   ° C

A temperatura no interior da câmara é:

T ∞ = 127   ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas barras de alumínio k = 176 W m . K de 5 cm de diâmetro e 15 cm de comprimento, com superfícies ásperas são pressionadas uma contra a outra com uma pressão de 20 atm. As barras estão em voltas em
Uma sala com temperatura do ar a 20 ℃ ℃ está perdendo calor para o ar externo a 0 ℃ ℃ a uma taxa de 1.000W através de uma parede de 2,5m de altura e 4m de comprimento. Agora a parede é isolada com 2c
As paredes de um armazém de alimento são constituídas por uma camada de madeira ( k = 0,1W / m ⋅ K ) de 2c m de espessura em contato com uma camada de espuma de poliuretano k = 0,03W / m ⋅ K de 5c m d
As cafeterias frequentemente servem café em copos de papel que têm invólucro de papel ondulado, como mostrado a seguir. Esse invólucro de papel ondulado:a) Mantém o café quente.b) Aumenta a resistênci
Uma parede plana de tijolo k = 0,7W / m ⋅ K tem 10c m de espessura. A resistência térmica dessa parede por unidade de área éa) 0,143m 2 ⋅ K / W b) 0,250m 2 ⋅ K / W c) 0,327m 2 ⋅ K / W d) 0,448m 2 ⋅ K