Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Munson, Mecânica dos Fluidos- Ed: 4º - Capítulo 5.Problemas - Ex. 16

Um perfil de velocidade adequado para descrever o escoamento turbulento em tubos é...

V = u c R - r R 1 n i ^

Onde u c é a velocidade na linha de centro do tubo, r é a coordenada radial, R é o raio do tubo e i ^ é o versor alinhado com a linha de centro do tubo. Determine a razão entre a velocidade média, u - , e a velocidade no centro, u - c , para (a) n = 4 , (b) n = 6 , (c) n = 8 e (d) n = 10 .

Passo 1

Bom! Bora pra luta, meus queridos!

Bora começar fazendo um esboço da seção transversal desse tubo, pra entender o que tá acontecendo!

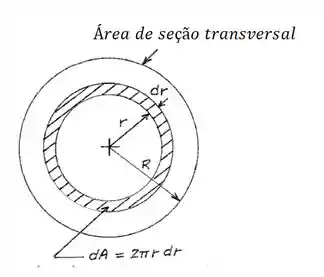
Vimos na teoria que para um volume de controle, o que entra tem que ser igual ao que sai.

Assim, usando a seguinte fórmula do balanço de massa...

m ˙ = ρ A u - = ∫ A ρ V → n ^ d A

Sendo assim, temos que...

V → n ^ = V → i ^ = u c R - r R 1 n i ^

Passo 2

Assim, para uma densidade uniformemente distribuída dividida pela área A :

u - = ∫ 0 R u c R - r R 1 n 2 π r d r π R 2

Isolando u - / u c :

u - u c = 2 ∫ 0 R 1 - r R 1 n r R d r R

Essa integral aí, considerando que...

x = r R

Seria o mesmo que escrever que...

u - u c = 2 ∫ 0 R 1 - x 1 n x d x

u - u c = 2 ∫ 0 R 1 - x 1 n x n 1 n d x

u - u c = 2 ∫ 0 R x n - x n + 1 1 n d x

Dessa forma, obtemos que...

u - u c = 2 n 2 2 n 2 + 3 n + 1

Passo 3

Calculando então, para...

  • n = 4

    • u - u c = 2 ⋅ 4 2 2 ⋅ 4 2 + 3 ⋅ 4 + 1

    u - u c = 0,711

  • n = 6

    • u - u c = 2 ⋅ 6 2 2 ⋅ 6 2 + 3 ⋅ 6 + 1

    u - u c = 0,791

  • n = 8

    • u - u c = 2 ⋅ 8 2 2 ⋅ 8 2 + 3 ⋅ 8 + 1

    u - u c = 0,837

  • n = 10

u - u c = 2 ⋅ 10 2 2 ⋅ 10 2 + 3 ⋅ 10 + 1

u - u c = 0,866

Resposta

n = 4 ⇒ u - u c = 0,711

n = 6 ⇒ u - u c = 0,791

n = 8 ⇒ u - u c = 0,837

n = 10 ⇒ u - u c = 0,866