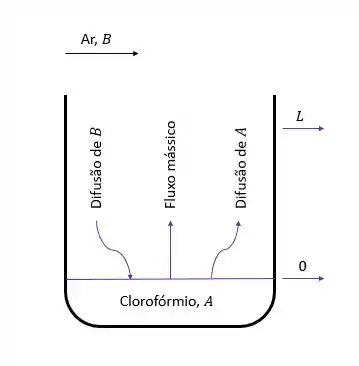
Um pesquisador está usando um tubo de Stefan de de diâmetro para medir a difusividade da massa de clorofórmio no ar a e . Inicialmente, a superfície do clorofórmio líquido foi de a partir da parte superior do tubo e, depois de horas, chegou a , o que corresponde a de clorofórmio sendo difundido. A , a pressão de vapor de clorofórmio é , e a concentração de clorofórmio é zero na parte superior do tubo. Considerando que a massa molar de clorofórmio é , determine a difusividade da massa de clorofórmio no ar.

Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:

• Vapor de clorofórmio e ar atmosférico são gases ideais.
• A quantidade de ar dissolvido no clorofórmio líquido é desprezível.
• Temperaturas do ar e do clorofórmio se mantém constantes a .

De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.

A fração molar do vapor de clorofórmio na interface é determinada da seguinte maneira:

A densidade molar total no tubo inteiro permanece constante, e isso se deve às condições de temperatura e pressão serem constantes também. Ela é determinada da seguinte forma:

A taxa de difusão dada vale por . Então a taxa de difusão por unidade de área da interface é:

E então, a difusividade mássica de clorofórmio no ar é determinada assim: