Uma placa circular com diâmetro de é mantida perpendicular à um jato horizontal axissimétrico de ar que apresenta velocidade e diâmetro iguais a e . Um furo no centro da placa cria um outro jato de ar que também apresenta velocidade igual a mas de diâmetro. Determine a componente horizontal da força necessária para imobilizar a placa circular.

Passo 1
E aí, galerinha! Oia nós aqui de novo!
Mais um exercício de conservação de massa!
Como é de costume, vamos começar fazendo um esboço do volume de controle e destacando os aspectos mais importantes do nosso sistema:
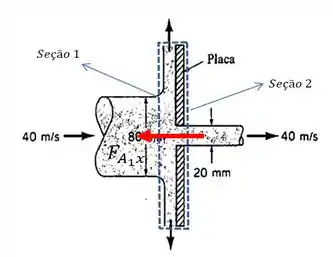
Dessa forma, aplicando a fórmula da conservação de massa ao longo do volume de controle, temos que...
E quando a gente tá falando em volume de controle e conservação de massa... Considerando o nosso escoamento como incompressível, temos que a vazão vai ser a mesma ao longo de todo o fluxo do líquido...
Passo 2
Assim, aplicando a equação de força para os componentes em , temos que...
Como :
Passo 3
Agora, substituindo os valores numéricos podemos obter a força desprendida: