Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 24
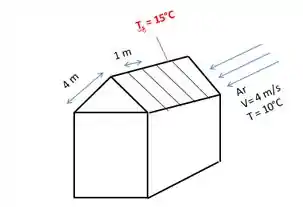
Placas paralelas formam um coletor solar que cobre um telhado, como mostrado na figura abaixo. As placas são mantidas a 15ºC, enquanto o ar ambiente a 10ºC escoa ao longo do telhado com V = 4 m/s. Determine a taxa de perda de calor convectiva da (a) primeira placa e (b) da terceira placa.
Passo 1
Pensa aqui comigo rapidinho nessa questão. A gente quer saber a taxa q que sai nas placas especificadas, correto? Então se a gente conseguir identificar em qual posição o escoamento começa a mudar de regime (posição Xc), poderíamos então decidir qual correlação vamos usar em cada placa, e, essa posição está relacionada com o Reynold crítico para placa plana, olha só...
Vamos antes pegar as propriedades do ar em Tf para adiantar nossa vida, beleza?
Vamos substituir esse paranauê todo pra descobrir logo nosso Xc!
O que isso significa? Que só depois de percorrido 1,81 m é que o escoamento começa a passar de laminar para turbulento!
Passo 2
(a) Queremos calcular a taxa na primeira placa, ou seja, com L = 1 m, e como vimos anteriormente, o comprimento crítico é em 1,81 m, então para a primeira placa estamos no regime laminar ainda, belê?
Então vamos usar uma correlação apropriada que é:
Bora calcular o Reynold para a primeira placa:
OBS: Perceba que aqui a gente encontrou um Reynold menor que o Reynold crítico, então tá fazendo sentido!!
E agora é só a gente substituir na equação de convecção e ser feliz ;)
Passo 3
(b) Para a 3ª placa já estaremos em L = 3m de distância do bordo de ataque, então já estamos além do Xc, ou seja, estamos agora no regime combinado turbulento e laminar e basta usar uma nova correlação para esse regime, e recalcularmos o novo Reynold, sacou?
E agora é só substituir no q de convecção e pronto, exercício terminado, certo? NÃOOOOOOOOOOOO!!!!!
Percebe que a gente calcular com L=3 m, certo? Então quando a gente faz isso é como se estivéssemos falando que a placa que estamos analisando tem 3 m, quando na verdade tem apenas 1 m. Então o que a gente tem que fazer?
Bem, a gente vai fazer o mesmo procedimento só que agora calculando o h para a 2ª placa.
Você concorda comigo que se a gente fizer uma subtração entre o valor calculado para L = 3 m
com e L = 2 m, vamos ter exatamente a taxa trocado pela 3ª placa? Então, bora pras contas!!
Passo 4
Vamos calcular a diferença entre os q para cada L, beleza?
Onde W = 4 m (largura da placa)
IMPORTANTE: Esses resultados fazem sentido?
E a resposta é SIMMM! Com o andar do fluido no eixo x da placa, mais próximas as temperaturas vão ficando, ou seja, mais próximo do equilíbrio térmico estamos chegando, e a força motriz para que haja troca térmica é exatamente a diferença de temperatura. Então é de esperar que o calor perdido na 3ª placa seja realmente menor do que na 1ª placa.