Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 105

O telhado da casa é constituído por laje de concreto ( k = 1,4 w m ∙ k e α = 0,69 × 10 - 6 m 2 s )   de 15   c m de espessura, 18   m de largura e 32   m de comprimento. No fim da tarde, às 18 horas, a laje apresenta temperatura uniforme de 18   ° C . As temperaturas médias do ar ambiente e do céu noturno a noite toda são 6   ° C e 260   K , respectivamente. Os coeficientes de transferência de calor por convecção nas superfícies interna e externa do telhado podem ser considerados h i = 5 e h o = 12 W m 2 ∙ K , respectivamente. A casa e as superfícies internas das paredes e do piso são mantidas a uma temperatura constante de 20   ° C durante a noite, e a emissividade de ambas as superfícies do telhado de concreto é 0,9 . Considerando as transferências de calor por radiação e convecção e utilizando o método explícito de diferenças finitas com passo de tempo ∆ t = 5   m i n e tamanho da malha de ∆ x = 3   c m , determine as temperaturas das superfícies interna e externa do telhado às 6 horas da manhã. Além disso, determine a taxa média de transferência de calor através do telhado durante a noite.

Passo 1

A partir do enunciado podemos retirar os seguintes dados:

k = 1,4 W m ∙ K ;   α = 0,69 × 10 - 6 m 2 s ; T i = 20 ° C ; T p a r e d e = 293   K ; T o = 6 ° C ; T c é u = 260   K

h i = 5 W m 2 ∙ K ; h o = 12 W m 2 ∙ K ;   ∆ x = 0,03   m ;   ∆ t = 5   m i n

Primeiramente, temos que encontrar o número de nós que vamos utilizar para analisar o telhado, e podemos fazer isso com a fórmula abaixo:

M = L ∆ x + 1 = 0,15 0,03 + 1 = 6

Portanto realizando uma representação dos nossos nós no telhado, teremos:

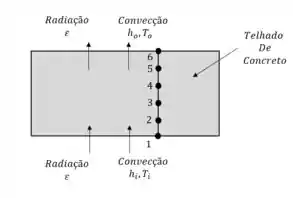
Passo 2

Note que os nós 1 e 6 são de contorno, e os restantes são internos, logo para os nós internos temos a seguinte formulação:

T m - 1 i - 2 T m i + T m + 1 i + e ˙ m i ∆ x 2 k = T m i + 1 - T m i τ

T m i + 1 = τ T m - 1 i + T m + 1 i + 1 - 2 τ T m i + τ e ˙ m i ∆ x 2 k

Passo 3

Agora podemos aplicar o balanço de energia no nós 1 e 6, e utilizar nossa equação para os nós internos...

N ó   1 :

h i T i - T 1 i + k T 2 i - T 1 i ∆ x + ε σ T p a r e d e 4 - T 1 i + 273 4 = ρ ∆ x 2 c p T 1 i + 1 - T 1 i ∆ t

N ó   2 :

T 2 i + 1 = τ T 1 i + T 3 i + 1 - 2 τ T 2 i

N ó   3 :

T 3 i + 1 = τ T 2 i + T 4 i + 1 - 2 τ T 3 i

N ó   4 :

T 4 i + 1 = τ T 3 i + T 5 i + 1 - 2 τ T 4 i

N ó   5 :

T 5 i + 1 = τ T 4 i + T 6 i + 1 - 2 τ T 5 i

N ó   6 :

h o T 0 - T 6 i + k T 5 i - T 6 i ∆ x + ε σ T c é u 4 - T 6 i + 273 4 = ρ ∆ x 2 c p T 6 i - T 6 i ∆ t

Passo 4

Utilizando um passo de ∆ t = 5   m i n , indicado pelo exercício temos que:

τ = α ∆ t ∆ x 2 = 0,69 × 10 - 6 m 2 s 300   s 0,03   m 2 = 0,230

Substituindo o valor de τ em outras quantidades para se encontrar as temperaturas interna e externa às 6 horas da manhã:

P a s s o s   d e   t e m p o = 12 × 60 5 = 144   p a s s o s   d e   t e m p o

As temperaturas serão:

T 1 = 10,3 ° C

T 6 = - 0,97 ° C

Passo 5

Podemos encontrar a taxa média de transferência de calor durante a noite a partir da temperatura média, que pode ser calculada como:

T m é d i a = T 1 ,   18 h r s + T 1,6 h r s 2 = 18 + 10,3 2 = 14,15 ° C

Logo...

Q ˙ m é d i a = h i A s T i - T 1 , m é d i a + ε σ A s T p a r e d e 4 - T 1 i + 273 4

Q ˙ m é d i a = 5 w m 2 ∙ K 18 × 32   m 2 20 - 14,15 ° C + 0,9 18 × 32   m 2 5,67 × 10 - 8 W m 2 ∙ K 293   K 4 - 14,15 + 273   K 4

Q ˙ m é d i a = 33,640   W

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro