Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 102

Um trocador de calor de casco e tubo com 2 passes no casco e 8 passes no tubo é usado para aquecer álcool etílico c p = 2670 J k g . ° C nos tubos de 25°C a 70°C a uma taxa de 2,1 kg/s. O aquecimento deve ser feito com água c p = 4190 J k g . ° C que entra no casco a 95°C e sai a 60°C. Se o coeficiente geral de transferência de calor for de 800 W m 2 K , determine a superfície de transferência de calor utilizando (a) o método LMTD e (b) o método ε -NTU.

Passo 1

Shooow !!

Vamos começar mais umaa!!

Na letra (a) nós temos o método LMTD, e segundo ele podemos calcular a área da superfície como:

A s = Q ˙ U F ∆ T l m

O que nós temos ?

U = 800 W m 2 K

Complicou !! Vamos ter muitas coisas para achar, né? Mas vamos por partes!!

Começando pela transferência de calor:

Q ˙ = m a l c o o l ˙ c p , a l c o o l ( T f ,   s a i - T f ,   e n t r a )

Temos todos os dados, não é?

m a l c o o l ˙ = 2,1 k g s

c p , a l c o o l = 2670 J k g . ° C

T f ,   s a i = 70 ° C

T f ,   e n t r a = 25 ° C

Substituindo:

Q ˙ = 2 , 1 k g s 2670 J k g . ° C ( 70 ° C - 2 5 ° C )

Q ˙ = 252315   W

Passo 2

Belezaa!

Agora precisamos achar a variação da temperatura logarítima.

Para este trocador de calor:

∆ T l m = ∆ T 1 - ∆ T 2 ln ⁡ ∆ T 1 ∆ T 2

Usando o método LMTD:

∆ T 1 = T q ,   e n t r a - T f ,   s a i

∆ T 2 = T q ,     s a i - T f ,   e n t r a

Nós temos quase tudo:

T q ,   e n t r a = 9 5 ° C

T q ,     s a i = 6 0 ° C

T f ,   e n t r a = 2 5 ° C

T f ,     s a i = 70 ° C

Substituindo:

∆ T 1 = 9 5 ° C - 70 ° C = 25 ° C

∆ T 2 = 6 0 ° C - 2 5 ° C = 35 ° C

E a diferença logarítima:

∆ T l m = 25 ° C - 35 ° C ln ⁡ 25 ° C 35 ° C

∆ T l m = 29,7 ° C

Passo 3

Agora só precisamos achar o fator de correção, F !!

Para isso vamos olhar a figura abaixo:

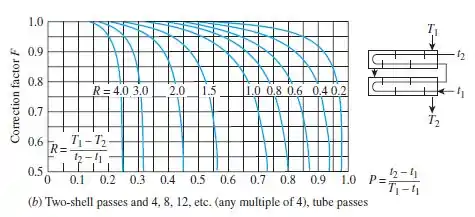
Então vamos começar calculando R e P:

R = T q ,   e n t r a - T q ,   s a i T f ,   s a i - T f ,   e n t r a = 95 ° C - 6 0 ° C 70 ° C - 25 ° C = 0,78

P = T f ,   s a i - T f ,   e n t r a T q ,   e n t r a - T f ,   e n t r a = 70 ° C - 25 ° C 95 ° C - 25 ° C = 0 , 64

Então:

F ≅ 0,93

Substituindo tudo na fórmula do Passo 1:

A s = 252315   W 800 W m 2 K ( 0,93 ) 29,7 ° C

A s = 11,4   m ²

E é isso aí galerinhaa!! Achamos a resposta da letra (a)!!

Passo 4

Na letra (b) vamos usar o método ε -NTU, vamos ver o que ele nos diz?

A s = N T U . C m i n U

Nós não temos N T U nem C m i n , certo?

Então vamos começar com C m i n , lembrando que:

C = m ˙ c p

Nós sabemos que:

C f = m á g u a ˙ c p = 2,1 k g s 2670 J k g . ° C = 5607 J s . ° C = 5607   W ° C

Agora precisamos achar para o fluido quente, certo?

Para acha-lo vamos usar a fórmula:

Q ˙ = C q ( T q ,   e n t r a - T q ,   s a i )

Substituindo:

252315   W = C q ( 95 ° C - 60 ° C )

C q = 7209   W ° C

Sendo assim:

C m i n = C f = 5607   W ° C

C m a x = C q = 7209   W ° C

Passo 5

E o próximo passo? Achar o NTU, certo?

Vamos olhar a figura abaixo:

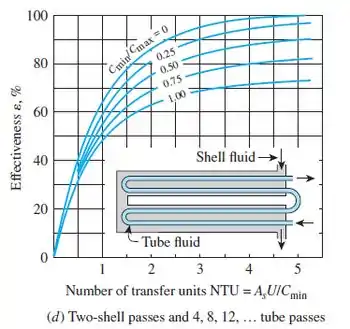
Já sabemos que:

C = C m i n C m a x

Então:

C = 5607   W ° C 7209   W ° C = 0 , 78

Agora o único dado que precisamos é a eficácia, se lembrarmos que:

ε = Q ˙ Q m a x ˙

Já temos:

Q ˙ = 252315   W

Agora só precisamos do valor máximo:

Q m a x ˙ = C m i n T q ,   e n t r a - T f ,   e n t r a

Q m a x ˙ = 560 7   W ° C 9 5 ° C - 2 5 ° C

Q m a x ˙ = 392490 W

E a eficiência?

ε = 252315   W 392490 W = 0 , 64

Olhando na figura acima:

N T U ≅ 1,7

Passo 6

Para finalizar com chave de ouro substituímos na fórmula do passo 4:

A s = 1,7 . 5607   W ° C 800 W m 2 K

A s = 11,9   m ²

E fiiim !!

Resposta

  1. A s = 11,4   m ² ;
  2. A s = 11,9   m ² .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

72 – A temperatura do fluido frio pode estar acima da temperatura de entrada do fluido quente em algum local do trocador de calor? Explique
77 - Considere um trocador de calor de casco e tubo para água-água com vazões mássicas idênticas para os fluidos quente e frio.Agora, a vazão mássica da água fria é reduzida pela metade.A efetividade
73 - Considere um trocador de calor no qual ambos os fluidos têm o mesmo calor específico, mas diferentes vazões mássicas. Qual fluido experimentara maior mudança de temperatura: aquele com menor ou m
75 – Em quais condições um trocador de calor de contracorrente pode ter uma efetividade igual a 1?Qual seria sua resposta para um trocador de calor de escoamento paralelo?
81 – Considere um trocador de calor que tem N T U 0,1. Alguém propõe triplicar o tamanho do trocador de calor, e o N T U é triplicado para 0,3, a fim de aumentar a efetividade e, assim, poupar energia