Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 130
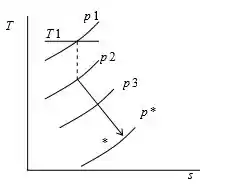
Um tubo de área constante é alimentado por um bocal somente convergente. O bocal recebe ar de uma grande câmara a e . O tubo possui um comprimento de atrito de , e é bloqueado na saída. Qual é a pressão na saída do tubo? Se do comprimento deste tubo é removido, e as condições na estação 1 e o fator de atrito permanecem constantes, qual é a nova pressão de saída e o novo número de Mach? Esboce ambos os processos em um diagrama
Passo 1
Fala aí, galera. Vamos para mais um problema de mecânica dos fluidos. Primeiramente, a estação 1 é um estado de estagnação, a estação 2 está entre o bico e o duto de fricção e a estação 3 está na saída do duto. Para a parte (a), sabemos:
Portanto, podemos fazer as seguintes declarações:
Portanto, o número Mach na entrada do duto é:
(Usamos o Solver para encontrar o número Mach correto para corresponder ao comprimento de atrito) A pressão na estação 2 pode ser encontrada a partir do número Mach e do estado de estagnação:
Passo 2
Continuando, como o estado 3 é o estado crítico, podemos encontrar a pressão no estado 3:
Para a parte (a), sabemos que se removermos 80% do duto:
Como sabemos o estado 2 e o comprimento de atrito do duto, podemos encontrar o estado 3:
Portanto, o número Mach na saída do duto é:
(Usamos o Solver para encontrar o número Mach correto para corresponder ao comprimento de atrito) Para encontrar a pressão de saída:
No estado 3, a razão de pressão é:
Passo 3
Esboçando o gráfico:
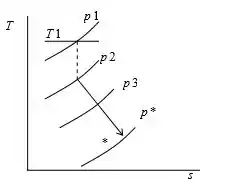
Resposta
