Você provavelmente deve ter percebido que balões inflados com gás hélio sobem no ar em um dia durante uma festa, mas caem no dia seguinte e agem como balões comuns cheios de ar. Isso ocorre porque o hélio no balão vaza lentamente para fora através da parede, enquanto o ar vaza por difusão.

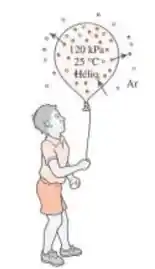
Considere um balão de borracha macia com 0,2 mm de espessura e 15 cm de diâmetro quando inflado. A pressão e a temperatura dentro do balão são inicialmente 120 kPa e 25°C. As permeabilidades da borracha ao hélio, oxigênio e nitrogênio a 25°C são , respectivamente. Determine as taxas iniciais de difusão de hélio, oxigênio e do nitrogênio através da parede do balão e a fração da massa de hélio que escapa do balão durante as primeiras 5 horas, assumindo que a pressão de hélio dentro do balão permaneça quase constante. Suponha que o ar tenha 21% de oxigênio e 79% de nitrogênio em número de mols e considere que as condições da sala são 100 kPa e 25°C.

E aí, galerinha ! Como vocês estão?

Animadoos, eu espero !!

Bom, a primeira coisa que precisamos descobrir são as taxas iniciais de difusão de hélio, oxigênio e do nitrogênio através da parede do balão, não é?

Como estamos trabalhando com gás nós usaremos:

Hora de ver o que sabemos, não é?

Se é a permeabilidade das espécies na borracha:

E das pressões? O que sabemos?

Como não há hélio no exterior nem oxigênio e nitrogênio no interior:

Agora é só achar as pressões dos gases no exterior e pronto!!

Bora ver as fórmulas?

Sabendo que no ar:

E:

Então:

Agora que temos tudo o que precisamos para achar as taxas iniciais:

Então nós temos o hélio saindo, enquanto o oxigênio e o nitrogênio estão entrando no balão, por isso o sinal negativo! :P

Bora pra próxima pergunta?