Enunciado
Física - Hewitt - Física Conceitual- Ed: 12º - Capítulo 2.Pense e Ordene - Ex. 35
2.35. Visto de cima, um toco firme é puxado por um par de cordas, cada qual com uma força de 200 N, mas em ângulos diferentes como mostrado. Ordene as forças resultantes sobre o toco, em ordem decrescente de valor.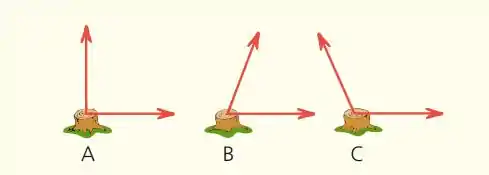 
Passo 1
Vamos calcular soma de vetores nessa questão aqui, e todas as forças no problema tem , mas a gente não sabe exatamente qual o ângulo das forças, então a gente não vai conseguir dizer exatamente o valor do módulo de cada resultante.
Então vamos comparar cada resultante. Vamos começar comparando o caso com o , usando a regra do paralelogramo para os dois casos:
Nesse caso . Olha só, como no caso um dos vetores se inclina em direção ao outro, eles se contribuem, os dois estão agindo no mesmo sentido, ai a força fica um pouco maior.
Passo 2
A gente sabe que , agora vamos comparar e .
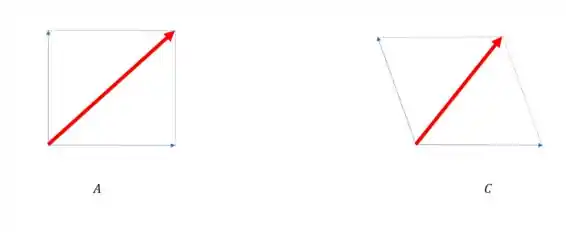
Agora a gente consegue ver que . No caso os vetores não se contribuem, mas se anulam, porque um vetor está inclinado no sentido oposto do outro, então uma partezinha do vetor é cancelada e ele fica menor.
Passo 3
Agora que sabemos que e , a gente pode organizar em ordem decrescente, do maior para o menor. O maior de todos é , uma vez que é maior que e é maior que , tem que ser maior que também. E então: