2.53. O que você pode afirmar corretamente sobre um par de vetores cuja soma é igual a zero?
Passo 1
Então temos um par de vetores, ou seja, dois vetores agindo no mesmo corpo, e sabemos que se a gente os somar o resultado vai ser zero.
Passo 2
Vamos pensar um pouquinho (como manda o livro). Suponha que tenha esse vetor agindo na caixa.

Você consegue imaginar como vai ser o outro vetor para a soma ser igual a zero? É esse aqui:
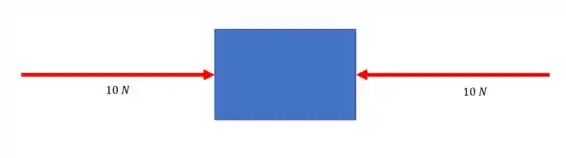
Esse vetor novo que a gente colocou tem o mesmo módulo, mesma direção, mas sentido diferente.
Vamos fazer outro exemplo:
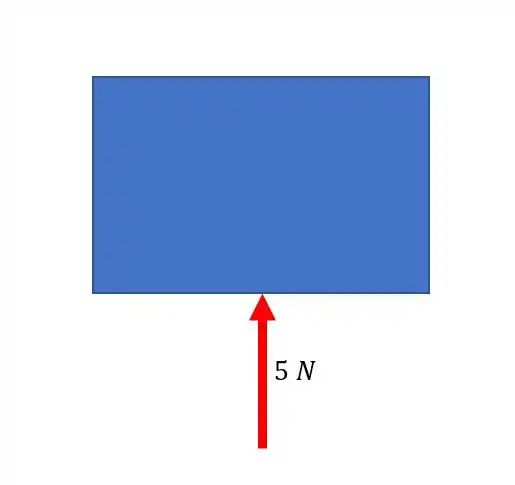
Agora nesse exemplo, qual vetor temos que colocar para somar vetorialmente com esse e ficar igual a zero?
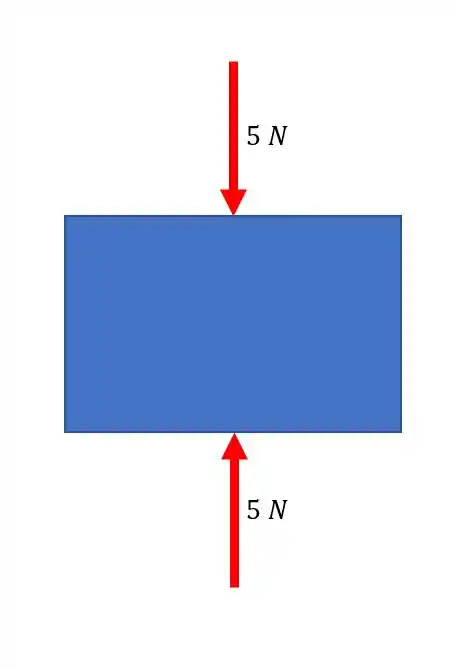
De novo, mesmo módulo, mesma direção e sentidos opostos.
Essa é a regra geral, a gente pode afirmar corretamente que o par de vetores que se somam vetorialmente e resultam em zero tem mesmo módulo, mesma direção, mas sentidos opostos.
Resposta
A gente pode afirmar corretamente que o par de vetores que se somam vetorialmente e resultam em zero tem mesmo módulo, mesma direção, mas sentidos opostos.