Enunciado
Física - Okuno - Física para Ciências Biológicas e Biomédicas- Ed: 1º - Capítulo 4.Problemas - Ex. 10
4.10. Alguns níveis energéticos de um átomo hipotético com um só elétron valem:
a. trace o diagrama de níveis de energia;
b. determine a energia necessária para ionizar esse átomo;
c. calcule o comprimento de onda mínimo da série que termina com n = 2;
d. calcule a energia necessária para excitar o átomo até n = 3;
e. de que comprimentos de onda se constitui o espectro de absorção?
Passo 1
Beleza, vamos lá.
Começando pelo item (a). O primeiro passo é desenhar linhas horizontais, cada linha representa um nível de energia:
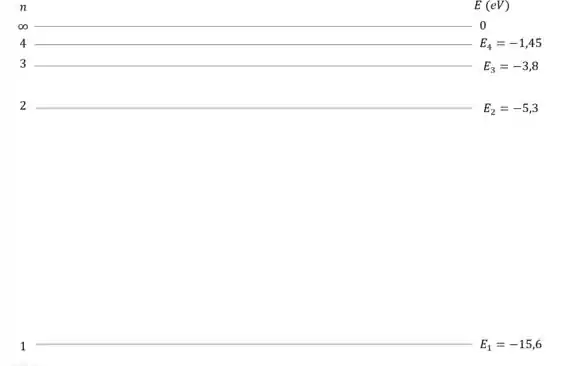
Para , a gente traça a linha correspondente a energia . A escala do diagrama está relacionada com a energia.
Essa é a parte fácil. A parte difícil são as setas verticais. Cada seta representa a frequência ou o comprimento de onda emitido por conta da mudança de estado.
Vamos calcular o comprimento de onda do fóton de uma mudança de para :
Por tanto:
Substituindo os valores:
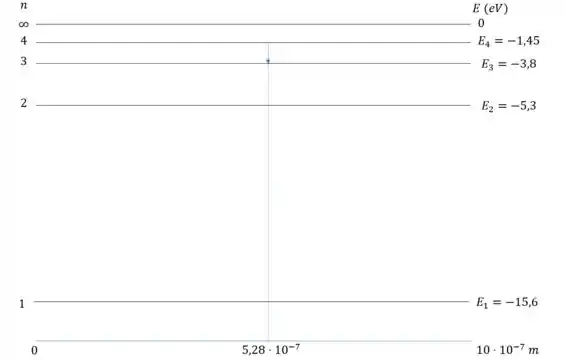
Agora a gente faz a mesma coisa para as outras mudanças:
Substituindo os valores:
E de para :
Substituindo os valores:
Então:
Agora, fazendo o mesmo processo para as outras mudanças, temos:
Finalmente, ficamos com:
Claro que você pode desenhar mais setas.
Passo 2
Agora vamos para o item (b).
Vamos supor que o elétron desse átomo se encontra no nível . Então, a energia necessária para ionizar o elétron é a mesma energia que leva o elétron do nível até o nível .
Nesse caso a energia é no mínimo , ou seja, . A mesma energia do nível , mas com o sinal oposto.
Passo 3
É a vez do item (c).
Vamos calcular o menor comprimento de onda para o nível .
O menor comprimento vai vir de até :
Substituindo os valores:
Passo 4
Chegamos ao item (d).
Então queremos excitar o átomo do estado fundamental até o nível . A energia necessária para fazer isso é dada pela equação:
Substituindo os valores:
Passo 5
E finalmente o último item.
Os comprimentos de onda variam mais ou menos de até . Esses comprimentos estão dentro do espectro infravermelho.
Resposta
- Infravermelho