Um alçapão quadrado em um teto tem de lado, uma massa de e está preso por uma dobradiça de um lado e por um ferrolho do lado oposto. Se o centro de gravidade do alçapão está a do centro em direção ao lado que está preso pela dobradiça, qual é o módulo da força exercida pelo alçapão (a) sobre o ferrolho e (b) sobre a dobradiça?
Passo 1
Vamos fazer um diagrama que representa a situação:
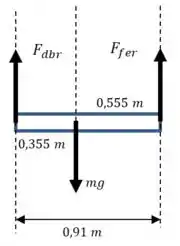
Nesse desenho, para calcular a distância entre (força exercida pela dobradiça) e o centro de massa, fizemos o seguinte:
E a outra distância é dada por:
Passo 2
(a) Temos três forças agindo em pontos diferentes de um corpo, e apenas uma (o peso) é conhecida.
Para calcular o módulo da força , vamos calcular o torque em relação ao ponto onde age:
As forças já são perpendiculares ao alçapão, então basta multiplicar o módulo pela distância até o ponto de referência:
Onde os sinais são trocados porque as duas forças favorecem a rotação em direções opostas:
Passo 3
Agora vamos fazer a mesma coisa para a outra força.
Dessa vez, vamos calcular o momento total em relação à extremidade direita do alçapão:
Mais uma vez, as duas forças já são perpendiculares ao alçapão, então:
Resposta
(a) A força sobre o ferrolho é de .
(b) A força sobre a dobradiça é de .