Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Eisberg e Resnick - Física quântica- Ed: 1º - Capítulo 11.Problemas - Ex. 7

N átomos distinguíveis estão distribuídos entre dois níveis de energia ε 1 = 0 e ε 2 = 0 .

A - Mostre que a energia do sistema é dada por:

E = N ε e - ε k T 1 + e - ε k T

B – Mostre que c v é dado por

c v = N k ε k T 2 e - ε k T 1 + e - ε k T 2

(Este é chamado de calor específico de Schottky e é observado, por exemplo, em sólidos paramagnéticos a baixas temperaturas; os níveis de energia correspondendo aos momentos magnéticos alinhados paralela e antiparalelamente a um campo magnético.)

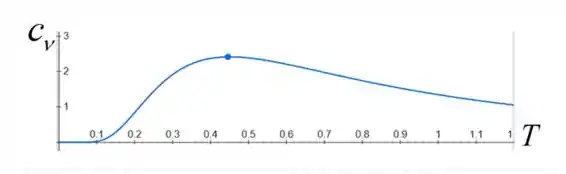
C- Faça um gráfico da dependência do calor específico com a temperatura, com a variação correta a altas e baixas temperaturas.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!

Para a letra a, a taxa entre o número de átomos com energia de nível 2 e o número de átomos com energia de nível é dado por:

n ε 1 n ε 2 = e - ε 2 - ε 1 k T

Substituindo ε por ε 2 e 0 para ε 1

n ε n 0 = e - ε k T

Manipulando para encontrar a expressão para n ( ε ) , nós temos:

n ε = e - ε k T n 0

O número de átomos distinguíveis em dois níveis de energia é:

n ε + n 0 = N

Com isso, nós temos:

e - ε k T + 1 n 0 = N  

Rearranjando para n(0):

n 0 = N e - ε k T + 1

Agora, nós podemos voltar a outra equação:

n ε = e - ε k T n 0 = N e - ε k T e - ε k T + 1

A energia total é dada por:

E = 0 ∙ n 0 + ε n ε = N ε e - ε k T 1 + e - ε k T

Com isso, provamos a letra a 😊

Passo 2

Para a letra b, a expressão de Debye para o calor específico de um sólido é igual a:

c v = d E d T

Substituindo N ε e - ε k T 1 + e - ε k T no lugar de E, nós vamos ter:

c v = d d t N ε e - ε k T 1 + e - ε k T  

A derivada desse termo dará algo do tipo:

c v = N ε e - ε k T ε k T 2 1 + e - ε k T 2

Manipulando um pouco mais, nós temos o seguinte resultado:

c v = N k ε k T 2 e - ε k T 1 + e - ε k T 2

Portanto, a expressão da letra b para o calor específico é provado.

Passo 3

Para a letra c, temos que pegar algumas coisas da letra b, como T → 0 , a capacidade do calor se aproxima e - ε k T T 2 e quando T → ∞ , a capacidade do calor tende a 1 T 2   . O gráfico mostra isso.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro