Quando um bloco de madeira for colocado no becker, o que acontecerá com a marcação da balança? Responda à mesma questão no caso de um bloco de ferro.
Passo 1
Essa aqui é bacana, hein? Bora pensar esse negócio juntos.
Repara que inicialmente foi colocado sobre a balança o bloco de madeira e o becker. Ou seja, a força normal (lembra que é isso que a balança mede) inicial vai ser:
Passo 2
Em seguida, o bloco de madeira foi posto dentro do becker. Dá uma olhada nas forças atuantes nesse sistema:
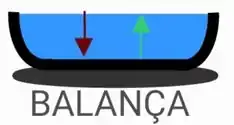
A seta para baixo é o peso do sistema e a para cima é a normal. Mas qual o peso do sistema? É o peso da madeira mais o peso do becker, né?
Não!
Cara, como a madeira flutua, existe uma força de empuxo ali compensando seu peso. Ou seja, o peso aparente do bloco de madeira será o peso real menos o empuxo.
Isso tudo pra te falar que a marcação na balança irá diminuir!
Passo 3
 Agora se liga no que acontece quando colocamos um bloco de ferro nesse becker.
Agora se liga no que acontece quando colocamos um bloco de ferro nesse becker.
Reparou naquela setinha que brotou do nada ali? Não se assusta quando eu te contar quem ela representa.
É o empuxo!
QUÊ? EMPUXO PARA BAIXO?
Então, meu amigo, tá lembrado das famosas leis de Newton? A terceira nos diz que para toda força de ação existe uma reação de mesmo módulo e sentido oposto. Quer dizer que a água empurra o bloco para cima, enquanto ele a empurra para baixo. E essas forças não se cancelam, pois atuam em corpos diferentes!
Beleza, mas por que isso importa? Dá uma olhada em como fica a expressão da força normal agora:
Ou seja, o bloco de ferro exerce uma força sobre o fundo do becker igual ao seu próprio peso. Logo, a marcação na balança não muda :D
Resposta
A marcação na balança irá diminuir.
A marcação na balança não será alterada.