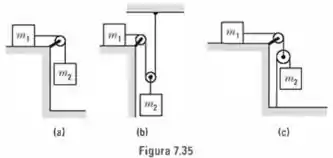
Calcule a aceleração dos corpos , e e a tensão nos fios (Fig. ). Despreze os atritos e as massas das polias. Qual dispositivo pode dar a uma aceleração maior do que a de queda livre? Resolva, ele início, algebricamente e, em seguida, aplique ao caso , .
Passo 1
E aí, beleza?? Para o item (a), temos as equações:
Somando as equações:
E a tração:
Passo 2
Agora, para o item (b), como temos uma polia móvel, vem:
Além disso:
Da segunda lei de Newton, vem:
Multiplicando a primeira equação por e somando, vem:
Ou seja:
Passo 3
Agora, para o item (c), vem:
Além disso:
Da segunda lei de Newton, vem:
Multiplicando a primeira equação por e somando, vem:
Ou seja:
Resposta
Note que apenas o sistema do item (c) pode fazer
(a)
(b)
(c)