Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 30.Exercícios e Problemas - Ex. 56
Um capacitor esférico, com um espaço de entre as esferas, tem capacitância igual a . Quantos valem os diâmetros das esferas?
Passo 1
Faaaaaala, galera... Tranquileba??
Fazendo um desenho da figura que o enunciado nos deu, temos:
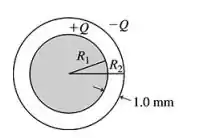
Como é pedido a capacitância, que por definição é:
Precisamos achar a diferença de potencial V. Como? Achando o campo eletrico no objeto. Sim! Veja:
Como achar o campo na esfera? Pela lei de Gauss, assim:
Considerando o campo eletrico constante:
Sabendo que a are ade uma esfera é:
Assim:
Assim temos o campo. Mas o enunciado nos dá informação do potencial, assim:
De modo que:
A diferença de potencial é dada pela diferença de potencial de um raio ao outro e é a diferença de potencial do raio interno até o externo. Fica fácil ver isso tomando a definição do fluxo elétrico para a Lei de Gauss que usamos.
Assim:
Logo:
Passo 2
De modo que:
É nos dado que , logo
Antes, temos que:
Assim, retornando à equação 0.1:
E sendo , então :
Passo 3
Pede o diâmetro, logo: