Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 35.Exercícios e Problemas - Ex. 58

Um capacitor de placas paralelas circulares com 4,0 cm de diâmetro, espaçadas por 1,0 mm, é previamente carregado a 1.000 V. Um interruptor é fechado em t 0 s, e o capacitor começa a descarregar através de um fio com 0,20 de resistência.

a. Obtenha uma expressão para a intensidade do campo magnético no interior do capacitor, em um ponto com r 1,0 cm, em função do tempo.

b. Desenhe o correspondente gráfico B versus t.

Passo 1

Suponha que o campo elétrico dentro do capacitor seja uniforme. Usei a lei de Ampere-Maxwell para encontrar o campo magnético.

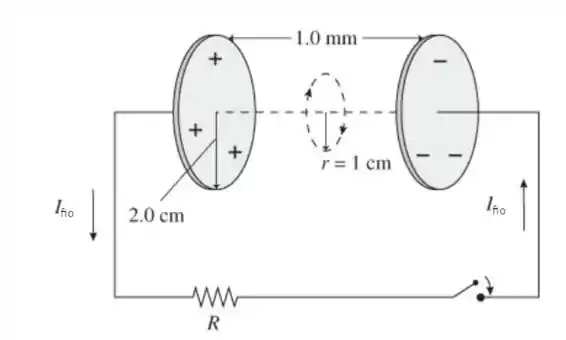
Passo 2

  1. Este é um circuito RC com capacitância C   =   ε 0 A / d   =   ε 0 π R ² / d   =   1.1 ∙ 10 ⁻ ¹ ¹   F   =   11.1   p F Nós sabemos a partir de Capítulo 32 que a corrente através do fio decai exponencialmente como

    2. I f i o   =   Δ V C R e - t / τ   =   ( 5000   A ) e - t / τ

    onde a constante de tempo é τ   =   2.22 ∙ 10 ⁻ ¹ ²   s   =   2.22   p s . O Exemplo 35.3 descobriu que o campo magnético induzido força no raio r dentro de um capacitor de carga ou descarga é

    B   =   μ 0 r 2 π R ² d q d t   =   μ 0 r 2 π R ² I f i o

    onde usamos I f i o   =   d Q / d t como a corrente real no fio que leva ao capacitor. Desta forma

    B     =   ( 4 π ∙ 10 ⁻ ⁷ ) ( 10 ⁻ ² ) 2 π ( 2 ∙ 10 ⁻ ² 0 5000 e - t / 2 . 22   =   ( 0.025 ) e - t / 2.22

    Passo 3

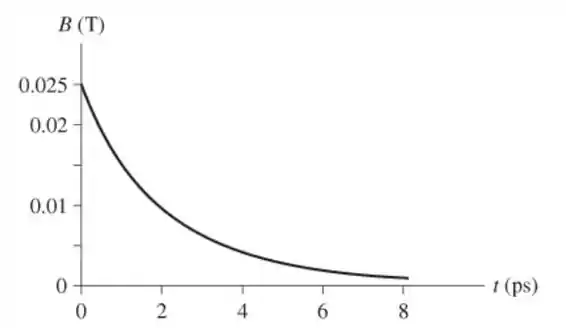
Resposta

ver a resolução

Ver Outros Exercícios desse livro