Enunciado
Física - Moysés - Vol. 3- Ed: 2º - Capítulo 2.Problemas - Ex. 7
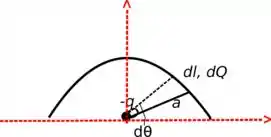
Uma carga Q é distribuída uniformemente sobre um fio semicircular de raio Calcule a força com que atua sobre uma carga de sinal oposto - colocada no centro (fig.).
Passo 1
Fala galerinha, beleza? Então, vamos começar pegando um pedaço muito pequeno desse fio, praticamente um infinitésimo que chamaremos de . Estamos fazendo assim, pois esse fio tem carga distribuída por ele todo. Sendo assim, nosso pedaço , corresponde a um pedaço de carga. Esse nosso dq é dado pela relação:
, para nossa distribuição geral de carga, nossa expressão fica
. Usamo pois estamos tratando de uma densidade linear de carga, varia de 0 a , pois trabalhamos com um semicírculo. Nossa carga total é da forma:
Essa distribuição dq contribui com um infinitésimo de força dF que age na carga situada no centro. As componentes x e y devem ser utilizadas em coordenadas polares na forma: {
A equação para a força eletrostática é da forma:
Onde esse r é dado pela soma dos componentes x e y em coordenadas polares.
Passo 2
Após saber essas etapas no passo 1, nós iremos trabalhar com toda álgebra envolvida rearranjando termos e fazendo uma integração em .
Resposta
Colocando “a” em evidência e organizando os termo e integrando de ambos os lados
o resultado da integral acima é 2 quando se aplica a substituição nos intervalos de 0 a . Lembrando no passo 1 que a distribuição total de carga Q é da forma podemos escrever como agora podemos substituir na força eletrostática e ficamos com a seguinte expressão:
.