Uma carga negativa fica em equilíbrio quando colocada no ponto médio do segmento de reta que une duas cargas positivas idênticas. Mostre que essa posição de equilíbrio é estável para pequenos deslocamentos da carga negativa em direções perpendiculares ao segmento, mas que é instável para pequenos deslocamentos ao longo dele.
Passo 1
Fala galera, tudo tranquilo? Bem, primeiramente precisamos analisar bem essa distribuição de carga. O que quer dizer que devemos fazer um pequeno esquema para saber como o sistema funciona.
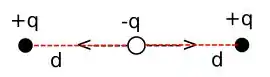
O que temos aqui é: duas cargas iguais “+q” e uma carga “-q” que se encontra exatamente no ponto médio entre as outras. Para essa configuração vou chamar as cargas escuras que estão nos extremos de q1 e q2, enquanto a carga no centro será q3.
Como a carga está em equilíbrio, podemos considerar que as forças exercidas na carga que está no centro são iguais. Deste modo, a força resultante desse sistema é nulaq1 (carga do lado esquerdo) q2 (carga do lado direito) e q3 (carga que se encontra no centro). São cargas de mesmo módulo, entretanto sinais contrários.
Nossa força resultante é da forma:
O sinal da força é negativo devido ao sentido que ela é exercida pelas setas pretas indicadas na imagem.
Com isso confirmamos que a força resultante é nula, uma vez que as suas cargas “+q” sejam concêntricas e a carga “-q” esteja no centro entre elas, nenhuma força vai fazer essa carga sair de sua posição inicial. Agora iremos analisar sob outro ponto no próximo passo.
Passo 2
Bem pessoal, esse passo a seguir é para analisarmos a situação de desequilíbrio.
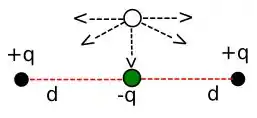
Nessa imagem estamos elevando a carga “-q” a uma altura bem pequena com distância “d”. A bolinha verde indica a posição anterior da carga. Observe que as componentes horizontais, são nulas assim como antes vistas no passo 1. Perceba também que a única componente que temos é essa que aponta para baixo na direção vertical, pois as componentes diagonais também se anulam.
O que nos leva a escrever a força resultante como uma componente de Y
Uma vez que os módulos das forças sejam iguais, temos
portanto
O que nos leva a perceber que a carga tende a voltar à sua configuração original
Passo 3
Agora iremos fazer o passo da terceira condição, a qual fala sobre o pequeno deslocamento na horizontal!
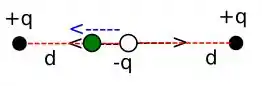
Agora a carga verde agora se encontra para a esquerda, a distância entre ela e a carga de cor branca é X, a distância da posição anterior da carga antes de ser movida para a esquerda, é d, desse modo, nossa distância atual é d-x. O deslocamento dessa carga para a esquerda altera a força exercida anteriormente pela carga q2 na carga q3. Pois, uma vez que essa posição muda a configuração das resultantes das forças, a força que a carga q2 exerce em q3, passa a ser menor. Já a força que a carga q1 que exerce em q3, agora é maior. Caso você ainda não tenha percebido, lembre-se que a distância influencia na força exercida sobre as cargas. Uma vez que a carga q3 está mais perto de q1, a força que q1 exerce em q3 passa a ser MAIOR. O que nos leva às seguintes forças. para a esquerda
para a direita
Resposta
Com isso, nossa resposta é exatamente o que conseguimos obter em todos os passos para cada caso.
Caso I
Caso II
Caso III
para a esquerda
para a direita