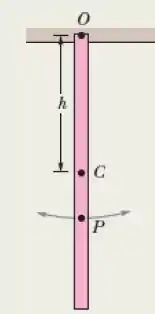
O centro de oscilação de um pêndulo físico possui a seguinte propriedade interessante: Se um impulso (horizontal e no plano de oscilação) é aplicado ao centro de oscilação, nenhuma oscilação é sentida no ponto de apoio Os jogadores de beisenol (e os jogadores de muitos outros esportes) sabem que, a menos que a bola se choque com o bastão nesse ponto (chamado de “ponto doce” pelos atletas), as oscilações produzidas pelo impacto serão transmitidas às mãos. Para demonstrar essa propriedade, use a régua da figura como modelo de um bastão de beisebol. Suponha que uma força horizontal (devido ao impacto da bola) age para a direita em , o centro de oscilação. O batedor segura o bastão em , o ponto de sustentação da régua. (a) Que aceleração a força imprime ao ponto ? (b) Que aceleração angular é produzida por em relação ao centro de massa da régua? (c) Como resultado da aceleração angular calculada no item (b), qual é a aceleração linear do ponto ? (d) Considerando os módulos e orientações das acelerações calculadas nos itens (a) e (c), convença-se de que o ponto é, de fato, um “ponto doce”.

(b) Agora queremos calcular a acelerção angular gerada pela força . Vamos precisar da seguinte equação:

Onde é o torque da força , é o momento de inércia e é a aceleração angular.

O enunciado pediu para calcularmos essa aceleração em relação ao centro de massa da régua, então:

E para calcular o torque, precisamos da distângia entre (o centro de massa) e (o ponto de aplicação da força):

Nós sabemos que a distância entre o ponto de suspensão e o centro de oscilação (os pontos e ), no caso de uma régua, é:

E a distância entre o ponto de suspensão e o centro de massa () é:

Então a distância entre e (veja o desenho) é:

Agora é só substituir na fórmula de cima:

(c) Vimos que a barra gira em torno do centro de massa com aceleração angular . Como ponto está a uma distância do centro de massa, a sua aceleração devido a essa rotação é:

Como a força empurra a barra para a direita, ela gira no sentido anti-horário. Olhando para o desenho, podemos ver que isso fará com que o ponto tenha uma acelerção inicial para a esquerda.

Mas essa não é a única aceleração agindo sobre o ponto . No item (a), calculamos uma aceleração na mesma direção da força , ou seja, para a direita. Então:

(d) Pelos nossos resultados, a escolha do ponto para a aplicação da força realmente é útil.

Ela faz com que as duas acelerações e se cancelem naturalmente, garantindo que o ponto em que o batedor segura o taco (ou nesse caso, o ponto de suspensão da régua) permaneça estacionário.