Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 19.Exercício - Ex. 22
Um cilindro contém de hélio a uma temperatura .
- Qual é o calor necessário para aumentar a temperatura para enquanto o volume permanece constante? Faça um diagrama para esse processo.
- Se, em vez de manter o volume constante, a pressão do hélio fosse mantida constante, qual seria o calor necessário para aumentar a temperatura de para ? Faça um diagrama para esse processo.
- Qual é o fator responsável pela diferença obtida nos itens (a) e (b)? Em qual dos dois casos o calor é maior? O que ocorre com o calor adicional?
- Caso o sistema fosse um gás ideal, qual seria a variação de energia interna do item (a)? E da parte (b)? Como você compara as duas respostas? Por quê?
Passo 1
Olá, tudo bem? Vou ajudar você nessa aqui!
Borá lá?
Letra a)
Como o processo é a volume constante, podemos por meio da fórmula encontrar o calor.
Não podemos esquecer que a temperatura deve sempre estar na escala Kelvin! Mas também que quando falamos em variação, não importa se estamos na escala Kelvin ou Celsius, a variação é sempre a mesma.
Consultando a tabela de calores específicos no livro texto temos que para o hélio e a variação e temperatura é ou também .
Agora é só substituir na fórmula do calor:
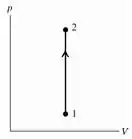
Agora vamos ao desenho do diagrama. Como se trata de um processo a volume constante, temos que o desenho será uma reta vertical indo do estado para o estado :
Passo 2
Letra b)
Como o processo agora é a pressão constante, podemos por meio da fórmula encontrar o calor.
Consultando a tabela de calores específicos no livro texto temos que para o hélio e a variação e temperatura é a mesma de .
Agora é só substituir na fórmula do calor:
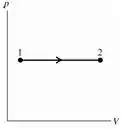
Agora vamos ao desenho do diagrama. Como se trata de um processo a pressão constante, temos que o desenho será uma reta horizontal indo do estado para o estado :
Passo 3
Letra c)
O calor é maior no processo à pressão constante. E eu posso explicar isso através da primeira lei, saca só.
A primeira lei nos diz que:
Certo? Mas em um processo a volume constante, como é o caso do item (a), sabemos que o trabalho realizado é nulo.
Esse calor adicional é justamente utilizado na expansão do gás.
Passo 4
Letra d)
Como temos um gás ideal, em ambos os casos temos que , como a variação de temperatura é a mesma, temos que em ambos processos a energia interna varia da mesma maneira.
Sendo assim, o calor vai ser maior no processo do item (b), pois temos que (numa expansão).
Resposta
