Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 35.Exercícios e Problemas - Ex. 61

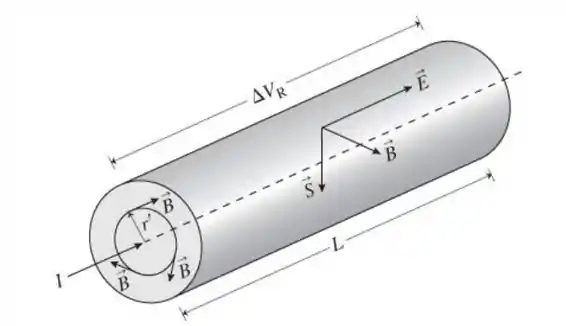
Considere uma corrente I que atravessa um resistor cilíndrico de

raio r, comprimento L e resistência R.

a. Determine os campos elétrico e magnético na superfície do re-

sistor. Suponha que o campo elétrico seja uniforme em todas as

partes, inclusive a superfície.

b. Determine a intensidade e a orientação do vetor de Poynting na

superfície do resistor.

c. Mostre que o fluxo do vetor de Poynting (isto é, a integral de

) sobre a superfície do resistor é igual a I2R. Depois dê uma

interpretação deste resultado.

Passo 1

  1. O campo elétrico E no resistor é

    2. E   =   Δ V R L   =   I   R L   =   E s u p e r f í c i e  

    para o campo magnético, nós iremos utilizar a lei de Ampere-Maxwell:

    ∮ B ∙ d s   =   μ 0 I a t r a v é s   =   μ I   ⇒   B ( 2 π r )   =   μ 0 I   ⇒   B   =   μ 0 I 2 π r   =   B s u p e r f í c i e  

    Passo 2

  2. O vetor de Poynting S = μ 0 E   ×   B é direcionado para a superfície curva. Ou seja, no fio. A grandeza é

    3. S   =   1 μ 0 E B   =   1 μ 0 I R L μ 0 I 2 π r   =   I ² R 2 π r L

  3. O fluxo sobre a superfície do resistor é

∫ S ∙ d A   =   ∫ f a c e S ∙ d A   +   ∫ p a r e d e S ∙ d A   =   0   +   S A p a r e d e   =   I ² R 2 π r L ( 2 π r L )   =   I ² R  

O vetor de Poynting é a potência por unidade de área transportada por campos elétricos e magnéticos. Assim, o fluxo de Poynting é a potência eletromagnética direcionada para o resistor. Corresponde à potência dissipada pelo resistor (I²R), que é o que esperamos da conservação de energia.

Resposta

Ver o desenvolvimento.

Ver Outros Exercícios desse livro