Uma corda é usada para puxar um bloco de com velocidade constante, por, em um piso horizontal. A força que a corda exerce sobre o bloco é , acima da horizontal. Quais são (a) o trabalho realizado pela força da corda, (b) o aumento na energia térmica do sistema bloco-piso e (c) o coeficiente de atrito cinético entre o bloco e o piso?

b) A figura abaixo ilustra as forças que agem sobre o bloco:

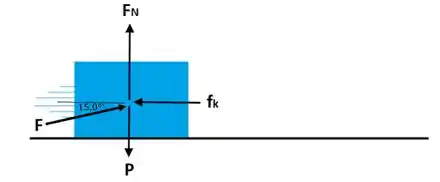
Vamos decompor a força F em duas componentes, uma no eixo x e outra no eixo y:

Sendo as forças que agem na horizontal apenas a e a força de atrito vamos aplicar a segunda lei de Newton, já que o bloco se movimento com aceleração temos que a força resultante é igual a zero:

Desta forma,

O aumento de energia térmica é dado por:

Assim, teremos

c) Em relação as forças verticais, temos a componente vertical da força exercida pela corda , a força peso e a força de reação normal ao piso . Vamos aplicar a segunda lei de Newton no eixo e, já que na vertical não há movimento então a força resultante é igual a zero:

Assim,

Sabendo que , podemos obter o valor do coeficiente de atrito cinético entre o bloco e o piso: