Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Eletromagnetismo- Ed: 5º - Capítulo 19.Problemas - Ex. 69
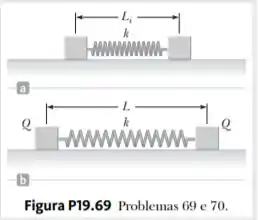
Dois blocos idênticos que descansam em uma superfície horizontal sem atrito estão ligados por uma mola leve possuindo uma constante elástica de e um comprimento natural de como mostra a Figura P19.69a. Uma carga é lentamente colocada em cada bloco fazendo com que a mola se estique para um comprimento de equilíbrio , conforme mostra a Figura P19.69b. Determine o valor de , modelando os blocos como partículas carregadas.
Passo 1
Resolver esse problema é bem tranquilo: para que o sistema fique em equilíbrio, a força de repulsão eletrostática deve anular a força elástica da mola:
Assim, na situação da figura b:
Lembre-se que
Portanto,
Assim, tirando a raiz
Passo 2
Substituindo os valores:
Portanto,
Ou ainda,