Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Campos e Ondas- Ed: 2º - Capítulo 14.Problemas - Ex. 29

Duas cargas de ponto positivo, cada uma com magnitude q, são fixados no eixo Y nos pontos y = a e y = —a. a) desenhe um diagrama mostrando as posições das cargas. (b) Qual é o potencial na origem? (c) Mostre que o potencial em qualquer ponto no eixo X é

V = 2 q 4 π ϵ 0 a 2 + x 2

(d) Esboce um gráfico do potencial no eixo X em função de x ao longo do intervalo de x = 5a até x = —5a. (e) Em que valor de x é a metade do potencial da origem? (f) De (e), obtenha o campo elétrico no eixo X.

Passo 1

E ai gente, beleza?

Vem comigo fazer essa questão aqui!

Letra a:

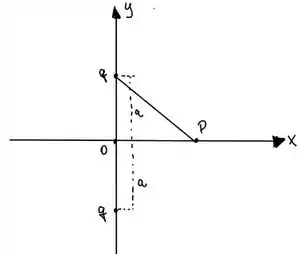
Passo 2

Letra b:

V 0 = 1 4 π ε 0 × q a + q a

V 0 = q 2 π ε 0 a V

Passo 3

Letra c:

V p = 1 4 π ε 0 x q a 2 + x 2 + q a 2 + x 2

V p = q 2 π ε 0 × a 2 + x 2

v p = 2 q 4 π ε 0 a 2 + x 2

v p = 2 q 4 π ε 0 x 2 + a 2

Passo 4

Letra d:

V p = k x 2 + a 2

Onde, k = 2 q 4 π ε 0 .

Daí podemos montar o gráfico:

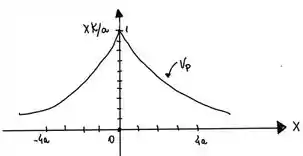
Passo 5

Letra e:

1 2 V 0 = V p q 4 π ε 0 a = 2 q 4 π ε 0 x 2 + a 2

x 2 + a 2 = 2 a → x 2 + a 2 = 4 a 2 x 2 = 3 a 2 → x = ± a 3

x = ± 1.7321  a

E podemos achar o campo elétrico a partir da letra c:

E = - g r a d V p E = - d V p d x

E = - d d x 2 q 4 π ε 0 ⋅ x 2 + a 2 → E = - 2 q 4 π ε 0 ⋅ d d x 1 x 2 + a 2

E = - 2 q 4 π ε 0 × - x x 2 + a 2 3 → E = 2 q x 4 π ε 0 x 2 + a 2 3

E = q x 2 π ϵ 0 a 2 + x 2 3

Resposta

  1. Ver gráfico
  2. V 0 = q 2 π ε 0 a V
  3. v p = 2 q 4 π ε 0 x 2 + a 2
  4. Ver gráfico
  5. E = q x 2 π ϵ 0 a 2 + x 2 3
Ver Outros Exercícios desse livro